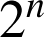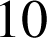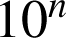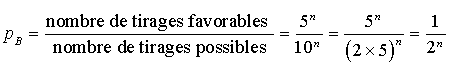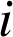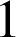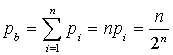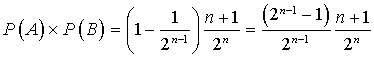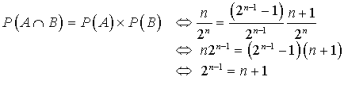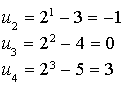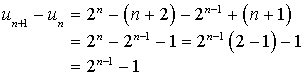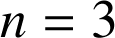Introduction
Durée : 50 minutes
Niveau : moyen
Une urne contient
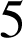 boules noires et
boules noires et
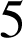 boules blanches.
boules blanches.
On en prélève
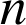 successivement et avec remise,
successivement et avec remise,
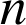 étant un entier naturel supérieur ou égal à
étant un entier naturel supérieur ou égal à
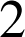 . On suppose les tirages équiprobables.
. On suppose les tirages équiprobables.
On considère les deux événements suivants :
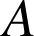 : « on obtient des boules des deux couleurs »,
: « on obtient des boules des deux couleurs »,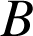 : « on obtient au plus une boule blanche ».
: « on obtient au plus une boule blanche ».
1)
a. Calculer la probabilité de l'événement : « toutes les boules tirées sont de la même couleur ».
b. Calculer la probabilité de l'événement : « on obtient exactement une boule blanche ».
c. En déduire les probabilités de ![]() ,
, ![]() et
et ![]() .
.
3) Soit la suite
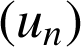 définie pour tout
définie pour tout
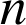 entier naturel supérieur ou égal à deux par :
entier naturel supérieur ou égal à deux par : ![]() .
.
Calculer
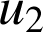 ,
,
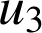 et
et
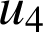 puis démontrer que la suite
puis démontrer que la suite
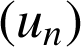 est strictement croissante.
est strictement croissante.
4) En déduire la valeur de l'entier
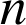 tel que les événements
tel que les événements
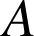 et
et
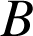 soient indépendants.
soient indépendants.