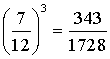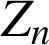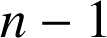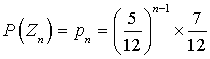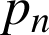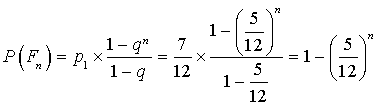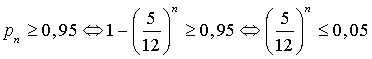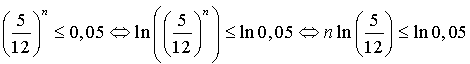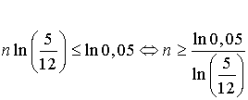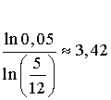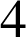Introduction
Durée : 40 minutes
Niveau : moyen
Une cible circulaire est composée de trois zones concentriques notées
,
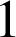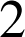et
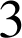. Les probabilités d'atteindre ces trois zones sont dans l'ordre :
,
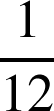et
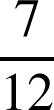. On admet que les résultats de plusieurs tirs successifs sont indépendants.
1) Quelle est la probabilité pour qu'un concurrent atteigne trois fois la zone
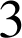en trois lancers successifs ?
2) Quelle est la probabilité qu'un concurrent atteigne les zones
,
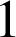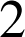et
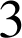dans cet ordre ?
3) Quelle est la probabilité qu'un concurrent atteigne les zones
,
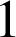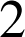et
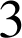dans n'importe quel ordre ?
4)
a. Pour 
, montrer que la probabilité 
qu'un concurrent atteigne la zone
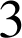pour la première fois au nième lancer est égale à 
.
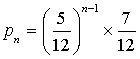b. Montrer que la suite
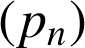est une suite géométrique dont on précisera la raison et le premier terme.
c. En déduire la probabilité de l'événement
« le concurrent atteint au moins une fois la zone
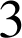en
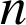lancers successifs ».
d. A partir de combien de lancers a-t-on 
?
