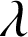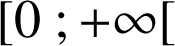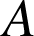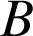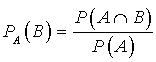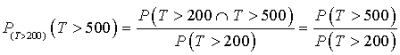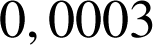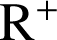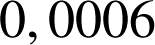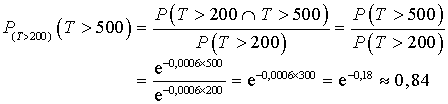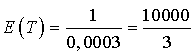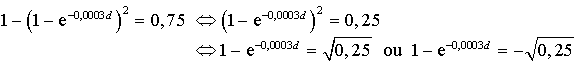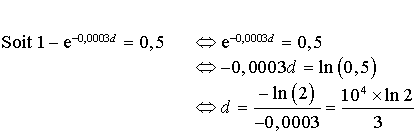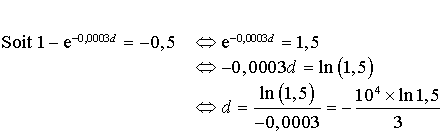Introduction
Durée : 40 minutes
Niveau : difficile
Une machine est équipée de deux composants identiques dont les durées de vie respectives
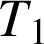et
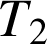(en jours) suivent la même loi exponentielle de paramètre
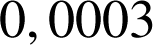. Lorsque ces deux composants sont montés en série la machine tombe en panne si l'un au moins des composants est défaillant. Lorsqu'ils sont montés en parallèle, la machine ne tombe en panne que si les deux composants sont défaillants. On admet l'indépendance des pannes des deux composants et on note
la durée de vie de la machine.
1) On suppose que le montage est fait en série :
a. Pour tout réel
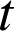positif, déterminer 
.
b. Quelle est la nature de la loi que suit la variable aléatoire
?
c. Quelle est la probabilité que la machine fonctionne au delà de
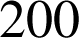jours ? On donnera la valeur exacte puis la valeur approchée à
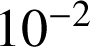près.
d. Sachant que la machine fonctionne depuis déjà
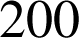jours, quelle est la probabilité qu'elle fonctionne encore au bout de
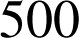jours ?
e. Quelle est la durée de vie moyenne d'une telle machine ?
2) On suppose que le montage est fait en parallèle :
a. Pour tout réel
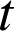positif, déterminer 
puis .
b.
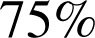des machines ont une durée de vie supérieure à
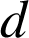jours, donner la valeur approchée à l'unité près de
.
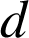