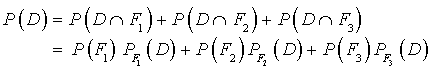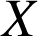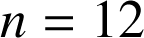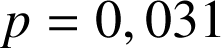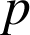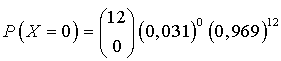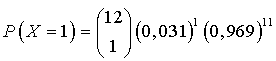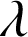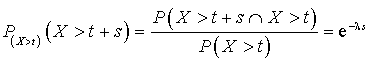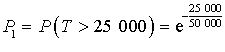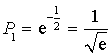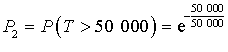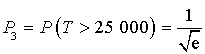Introduction
Durée : 60 minutes
Niveau : moyen
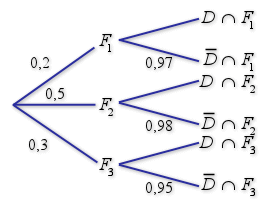
Un quincaillier achète des ampoules à trois fournisseurs dans les proportions suivantes :
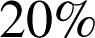au premier fournisseur,
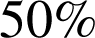au deuxième fournisseur et
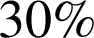au troisième fournisseur.
Le premier fournisseur fabrique
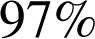des ampoules sans défaut, le deuxième fournisseur fabrique
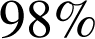d'ampoules sans défaut, le troisième fournisseur fabrique
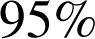d'ampoules sans défaut.
1) On choisit une ampoule au hasard dans le stock. On note
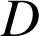l'événement « l'ampoule est défectueuse »,
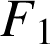l'événement « l'ampoule provient du premier fournisseur »,
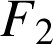l'événement « l'ampoule provient du deuxième fournisseur » et
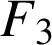l'événement « l'ampoule provient du troisième fournisseur ».
a. Calculer la probabilité de l'événement
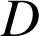, notée
.
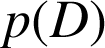b. Sachant que l'ampoule choisie est défectueuse, quelle est la probabilité
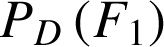qu'elle provienne du premier fournisseur ? Donner la valeur exacte et une valeur approchée à
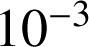près de
.
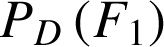2) On suppose que la probabilité qu'une ampoule soit sans défaut est de
.
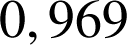On monte
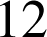ampoules sur un lustre. Calculer la probabilité
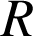qu'une ampoule au plus soit défectueuse. On donnera une valeur approchée à
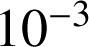près de
.
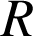3) La durée de vie en heures d'une ampoule, notée
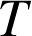, suit une loi de durée de vie sans vieillissement (ou loi exponentielle) de paramètre 
.
Selon cette loi, pour tout
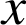de
, 
.
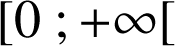a. Quelle est la probabilité
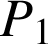qu'une ampoule dure plus de
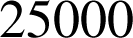heures ? Donner la valeur exacte de
.
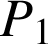b. Quelle est la probabilité
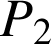qu'une ampoule dure plus de
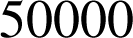heures ? Donner la valeur exacte de
.
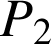c. Quelle est la probabilité
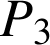qu'une ampoule dure plus de
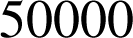heures sachant qu'elle a déjà duré
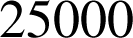heures ? Donner la valeur exacte de
.
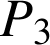