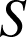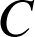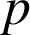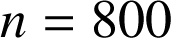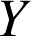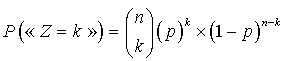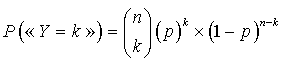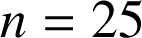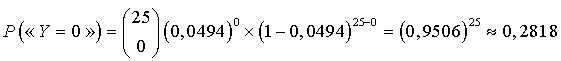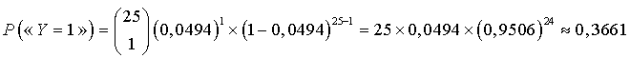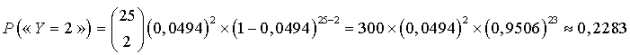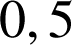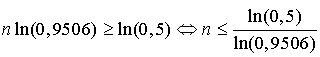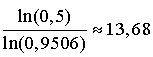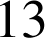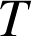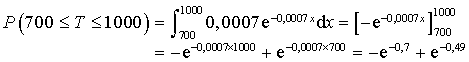Introduction
Durée : 60 minutes
Niveau : moyen
Une entreprise
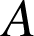est spécialisée dans la fabrication en série d'un article : un contrôle de qualité a montré que chaque article produit par l'entreprise
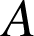pouvait présenter deux types de défaut : un défaut de soudure avec une probabilité égale à
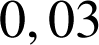et un défaut sur un composant électronique avec une probabilité égale à
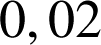. Le contrôle a montré aussi que les deux défauts étaient indépendants. Un article est dit défectueux s'il présente au moins l'un des deux défauts.
1) Montrer que la probabilité qu'un article fabriqué par l'entreprise
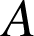soit défectueux est égale à
.
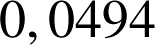2) Une grande surface reçoit
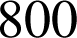articles de l'entreprise
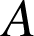. Soit
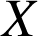la variable aléatoire qui, à cet ensemble de
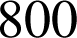articles, associe le nombre d'articles défectueux.
a. Définir la loi de
.
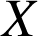b. Calculer l'espérance mathématique de
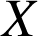. Quel est le sens de ce nombre ?
3) a. Un petit commerçant passe une commande de
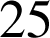articles à l'entreprise
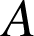. Calculer, à
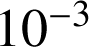près, la probabilité qu'il y ait au plus
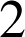articles défectueux dans sa commande.
b. Il veut que, sur sa commande, la probabilité d'avoir au moins un article défectueux reste inférieure à
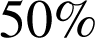. Déterminer la valeur maximale du nombre
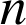d'articles qu'il peut commander.
4) La variable aléatoire qui, à tout article fabriqué par l'entreprise, associe sa durée de vie en jours, suit une loi exponentielle de paramètre
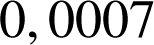, c'est-à-dire de densité de probabilité la fonction
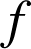définie sur 
par : 
. Calculer la probabilité, à
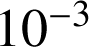près, qu'un tel article ait une durée de vie comprise entre
et
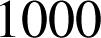jours.
