Introduction
Durée : 60 minutes
Niveau : moyen
Dans l'espace muni d'un repère orthonormal 
, on considère les points
,
,
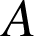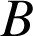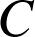et
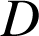de coordonnées respectives : 
, 
, 
, 
.
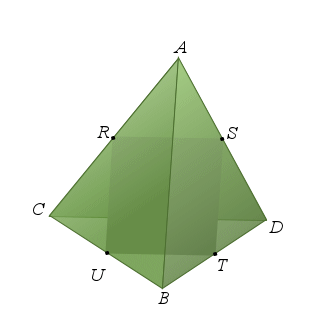
1) Démontrer que
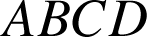est un tétraèdre régulier, c'est-à-dire un tétraèdre dont toutes les arêtes sont de même longueur.
Un tétraèdre régulier est un tétraèdre dont les six arêtes ont la même longueur.
A 1) Le calcul des six distances
,
,
,
,
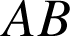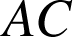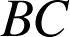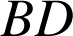et
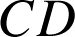conduit au même résultat :
.
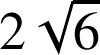En effet, 
.
.
2) On note
,
,
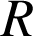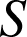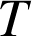et
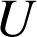les milieux respectifs des arêtes 
, 
, 
et 
.
Démontrer que
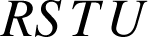est un parallélogramme de centre
.
Calculer les coordonnées des points
,
,
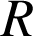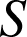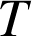et
.
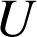A 2) Les coordonnées des points
,
,
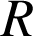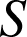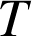et
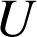sont :
; 
; 
; 
.
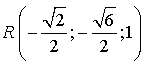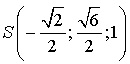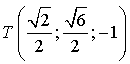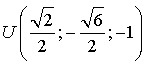Le milieu du segment 
a pour coordonnées
.
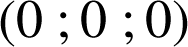Le milieu du segment 
a pour coordonnées
.
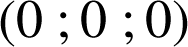Par conséquent et se coupent en leur milieu
et
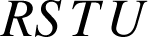est un parallélogramme de centre
.
3) Ce parallélogramme a-t-il des propriétés supplémentaires ? Expliquer.
On pourra utiliser le produit scalaire dans l'espace.
Montrer que
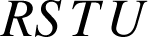est un carré.
A 3) Les coordonnées des vecteurs 
et 
sont : 
et 
.
On peut remarquer que : 
et que 
.
Par conséquent, le parallélogramme
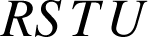est un carré.
On dispose de trois tétraèdres identiques au précédent, parfaitement équilibrés. Chacun d'eux a une face peinte en bleu, une face peinte en jaune et deux faces peintes en rouge.
On lance les trois tétraèdres simultanément (on remarquera que, lorsqu'on lance un tel tétraèdre, une seule face est cachée et trois faces sont visibles).
1) Calculer la probabilité qu'au moins trois faces rouges soient visibles sur les trois tétraèdres.
Il est plus simple de raisonner sur la face cachée.
B 1) Dans tous les cas au moins une face rouge est toujours visible pour chacun des tétraèdres ; donc la probabilité qu'au moins trois faces rouges soient visibles sur les trois tétraèdres est égale à
;
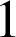2) Calculer la probabilité que la couleur bleue ne soit visible sur aucun tétraèdre.
On pourra examiner la face cachée sur un seul tétraèdre.
Les résultats obtenus sur les trois tétraèdres sont indépendants.
B 2) La couleur bleue n'est pas visible si elle est cachée pour chacun des trois tétraèdres.
Or les tétraèdres sont parfaitement équilibrés donc chacune des faces a la même probabilité d'être cachée soit
.
La probabilité que la face bleue soit cachée pour un tétraèdre est égale à
.
Les résultats obtenus sur les trois tétraèdres étant indépendants, la probabilité que la face bleue soit cachée pour les trois tétraèdres est égale à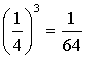 
.
3) Calculer la probabilité de l'événement
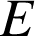: « les six faces rouges sont visibles ».
Les six faces rouges sont visibles lorsque les faces cachées sont bleues ou jaunes.
Calculer la probabilité que deux faces rouges soient visibles pour un seul tétraèdre.
B 3) Pour un tétraèdre, deux faces rouges sont visibles lorsque la face bleue ou la face jaune sont cachées ; par conséquent la probabilité que deux faces rouges soient visibles pour chacun des tétraèdres est égale à 
.
Les résultats obtenus sur les trois tétraèdres étant indépendants, la probabilité de l'événement
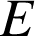est égale à 
.
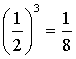4) On répète
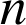fois l'expérience qui consiste à lancer les trois tétraèdres.
Calculer la probabilité
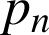que l'événement
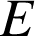soit réalisé au moins une fois.
Calculer 
.
Penser à examiner l'événement contraire de l'événement «
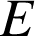est réalisé au moins une fois ».
Une expérience consiste à examiner si à l'issue du lancer des trois tétraèdres, six faces rouges sont visibles ou pas. C'est une épreuve de Bernoulli de paramètre
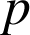égal à la probabilité de l'événement
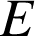donc 
.
On répète cette expérience
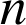fois de façon indépendante donc
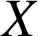qui désigne le nombre de fois que l'événement
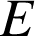est réalisé, suit une loi binomiale de paramètre
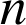et .
L'événement «
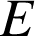est réalisé au moins une fois » est l'événement contraire de «
».
B 4) Une expérience consiste à examiner si à l'issue du lancer des trois tétraèdres, six faces rouges sont visibles ou pas. C'est une épreuve de Bernoulli de paramètre
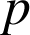égal à la probabilité de l'événement
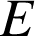donc .
On répète cette expérience
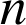fois de façon indépendante donc
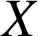, qui désigne le nombre de fois que l'événement
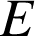est réalisé, suit une loi binomiale de paramètre
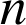et .
L'événement «
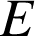est réalisé au moins une fois » est l'événement contraire de «
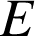n'est jamais réalisé », donc «
».
Or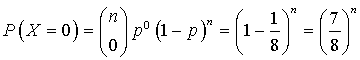 
.
Donc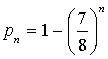 
.
Or 
, donc 
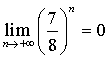et 
.
