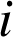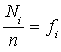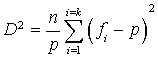Introduction
Durée : 60 minutes
Niveau : moyen
Énoncé de l'exercice :
Une expérience aléatoire qui conduit à
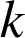 issues
issues ![]() dont les probabilités respectives sont toutes égales à
dont les probabilités respectives sont toutes égales à
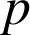 est réalisée
est réalisée
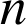 fois.
fois.
La formule théorique du
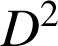
1) Pour ![]() et
et ![]() , on pose
, on pose ![]() la variable aléatoire égale au nombre de réalisation de l'issue
la variable aléatoire égale au nombre de réalisation de l'issue ![]() sur les
sur les
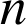 expériences. Donner la loi de
expériences. Donner la loi de ![]() et son espérance mathématique
et son espérance mathématique ![]() .
.
On répète de façon indépendante
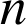 fois la même expérience.
fois la même expérience.
Une expérience est une épreuve à deux issues : obtenir le résultat ![]() avec la probabilité
avec la probabilité
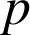 ou ne pas l'obtenir avec la probabilité
ou ne pas l'obtenir avec la probabilité ![]() .
.
Une épreuve conduit aux deux issues suivantes : soit le résultat ![]() est réalisé avec la probabilité
est réalisé avec la probabilité
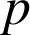 , soit il ne l'est pas avec la probabilité
, soit il ne l'est pas avec la probabilité ![]() .
.
On répète de façon indépendante cette épreuve, ![]() désigne le nombre de réalisations du résultat
désigne le nombre de réalisations du résultat ![]() ; par conséquent
; par conséquent ![]() suit la loi binomiale de paramètre
suit la loi binomiale de paramètre
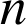 et
et
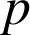 . D'où
. D'où ![]() .
.
2) Pour évaluer les écarts entre ![]() et
et ![]() , on introduit la variable aléatoire notée
, on introduit la variable aléatoire notée
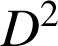 définie par :
définie par : 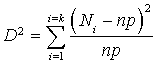 .
.
Vérifier que 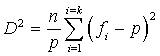 où
où ![]() désigne la fréquence d'apparition du résultat
désigne la fréquence d'apparition du résultat ![]() sur les
sur les
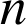 expériences.
expériences.
On pourra remarquer que
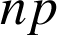 ne dépend pas de l'indice de sommation.
ne dépend pas de l'indice de sommation.
Écrire 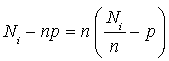 .
.
On répète 10 000 fois les
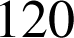 lancers d'un dé équilibré et on observe les valeurs
lancers d'un dé équilibré et on observe les valeurs
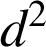 de
de
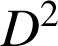 obtenues. Le tableau suivant donne le nombre de séries pour lesquelles la valeur de
obtenues. Le tableau suivant donne le nombre de séries pour lesquelles la valeur de
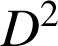 est strictement supérieure à l'entier
est strictement supérieure à l'entier
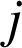 :
:
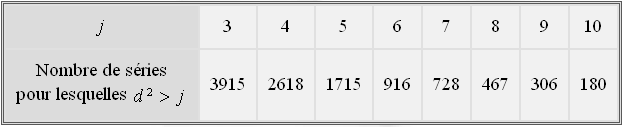
Déterminer la valeur
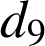 du
du
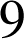 ème décile, puis celle
ème décile, puis celle
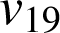 du
du
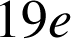 vingtile (ou
vingtile (ou
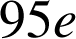 centile).
centile).
Revoir les définitions des déciles et vingtiles.
Par exemple : le neuvième décile est la plus petite valeur
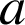 du caractère telle que les valeurs du caractère de
du caractère telle que les valeurs du caractère de
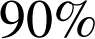 de la population étudiée soient inférieures ou égales à
de la population étudiée soient inférieures ou égales à
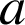 .
.
Le
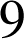 ème décile est la valeur
ème décile est la valeur
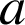 du caractère de la série telle que les valeurs du caractère de
du caractère de la série telle que les valeurs du caractère de
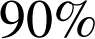 de la population étudiée soient inférieures ou égales à
de la population étudiée soient inférieures ou égales à
 ; ou encore
; ou encore ![]() .
.
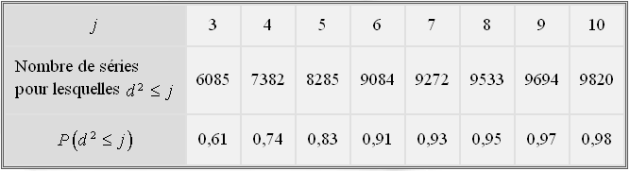
Ici pour
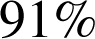 des
des
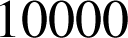 séries de lancers, on obtient
séries de lancers, on obtient ![]() , et pour
, et pour
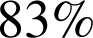 des
des
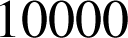 séries de lancers, on obtient
séries de lancers, on obtient ![]() .
.
Le neuvième décile est
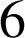 .
.
Ici pour
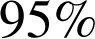 des
des
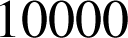 séries de lancers, on obtient
séries de lancers, on obtient ![]() , et pour
, et pour
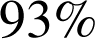 des
des
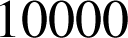 séries de lancers, on obtient
séries de lancers, on obtient ![]() .
.
Le dix-neuvième vingtile est
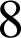 .
.
Le test du
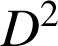
On réalise une expérience analogue avec un dé dont on souhaite tester la régularité.
Lorsque ![]() : on rejette l'hypothèse de régularité du dé au seuil de
: on rejette l'hypothèse de régularité du dé au seuil de
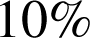 .
.
Lorsque ![]() : on rejette l'hypothèse de régularité du dé au seuil de
: on rejette l'hypothèse de régularité du dé au seuil de
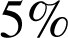 .
.
Parmi les
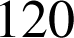 lancers, les
lancers, les
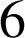 numéros sont sortis respectivement
numéros sont sortis respectivement
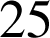 ,
,
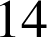 ,
,
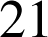 ,
,
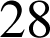 ,
,
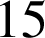 et
et
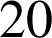 fois.
fois.
1) Calculer la valeur de
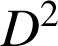 dans ce cas.
dans ce cas.
Dans ce cas ![]() ,
,
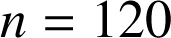 et
et ![]() .
.
1) 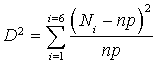 , ici
, ici
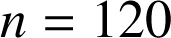 et
et ![]() d'où
d'où
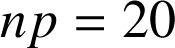 .
.
Le tableau des écarts est le suivant :

Donc ![]() .
.
On obtient ![]() .
.
2) Le dé est il régulier au seuil de
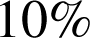 ? Au seuil de
? Au seuil de
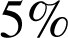 ?
?
On convient de rejeter la régularité d'un dé de façon significative au seuil de
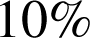 (ou de
(ou de
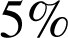 ) lorsque la valeur observée
) lorsque la valeur observée
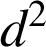 de
de
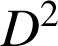 dépasse le
dépasse le
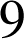 ième décile (ou le
ième décile (ou le
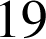 ième vingtile).
ième vingtile).
2) Pour le dé observé, ![]() .
.
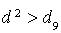 : au seuil de
: au seuil de
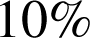 , on décide de rejeter l'hypothèse de régularité du dé.
, on décide de rejeter l'hypothèse de régularité du dé.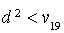 : au seuil de
: au seuil de
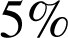 , on ne peut pas rejeter l'hypothèse de régularité du dé.
, on ne peut pas rejeter l'hypothèse de régularité du dé.
Application du test du
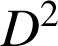
Une simulation a été réalisée sur une pièce de monnaie équilibrée, l'étude des valeurs
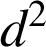 de
de
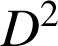 a permis de constater que le
a permis de constater que le
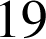 ème vingtile est égal à
ème vingtile est égal à
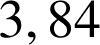 .
.
On lance une autre pièce de monnaie
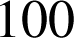 fois ; entre quelles valeurs doit être compris le nombre de faces obtenues pour que la pièce soit considérée comme équilibrée au seuil de
fois ; entre quelles valeurs doit être compris le nombre de faces obtenues pour que la pièce soit considérée comme équilibrée au seuil de
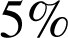 ?
?
Désigner par
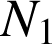 le nombre d'apparitions du côté face et par
le nombre d'apparitions du côté face et par
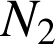 le nombre d'apparitions du côté pile.
le nombre d'apparitions du côté pile.
Exprimer
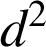 en fonction du nombre
en fonction du nombre
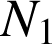 d'apparition du côté face, ne pas oublier que
d'apparition du côté face, ne pas oublier que ![]() .
.
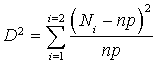 . Ici
. Ici
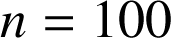 et
et
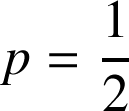 d'où
d'où
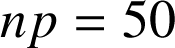 .
.
On désigne par
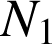 le nombre d'apparitions du côté face.
le nombre d'apparitions du côté face.
On désigne par
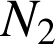 le nombre d'apparitions du côté pile.
le nombre d'apparitions du côté pile.
![]() or
or
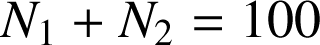 donc
donc
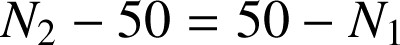 .
.
Par conséquent, ![]() .
.
Or le
 ème vingtile est égal à
ème vingtile est égal à
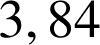 .
.
La pièce est donc considérée comme équilibrée au seuil de
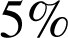 si et seulement si
si et seulement si ![]() .
.
![]()
Or ![]() et
et ![]() .
.
En conclusion, la pièce est considérée comme équilibrée au seuil de
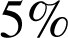 si et seulement si le nombre de faces obtenues est compris entre
si et seulement si le nombre de faces obtenues est compris entre
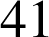 et
et
 .
.