Introduction
Durée : 90 minutes
Niveau : difficile
Énoncé de l'exercice
Introduction :
La durée de vie d'un individu est une variable aléatoire
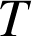 à valeurs dans
à valeurs dans ![]() où l'événement
où l'événement ![]() signifie que l'individu est vivant à l'instant
signifie que l'individu est vivant à l'instant
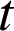 .
.
On suppose que cet individu n'est pas mort-né donc ![]() et il n'est pas certain que cet individu soit immortel donc il existe un entier
et il n'est pas certain que cet individu soit immortel donc il existe un entier
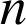 positif tel que
positif tel que ![]() .
.
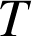 suit une loi de durée de vie sans vieillissement si la probabilité que l'individu soit vivant à l'instant
suit une loi de durée de vie sans vieillissement si la probabilité que l'individu soit vivant à l'instant
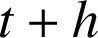 (
(
 ) sachant qu'il est vivant à l'instant
) sachant qu'il est vivant à l'instant
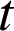 , ne dépend pas de
, ne dépend pas de
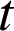 .
.
En formalisant on obtient :
pour tout
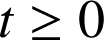 ,
, 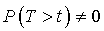 ,
,pour tout
 ,
,
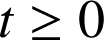 ,
, 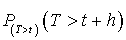 ne dépend pas de
ne dépend pas de
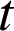 .
.
Objectif :
Le but de cet exercice est de prouver que
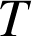 suit une loi exponentielle de paramètre
suit une loi exponentielle de paramètre
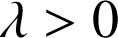 .
.
1) Montrer que : pour
 ,
,
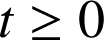 ,
, ![]() .
.
![]() ne dépend pas du choix de
ne dépend pas du choix de
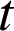 , choisir judicieusement
, choisir judicieusement
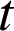 .
.
Définition :
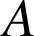 et
et
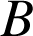 sont deux événements avec
sont deux événements avec ![]() .
.
La probabilité de l'événement
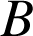 sachant
sachant
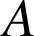 , notée
, notée ![]() est définie par :
est définie par : 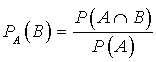 .
.
On pourra remarquer que :
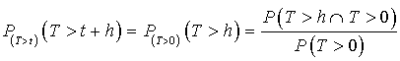 .
.
1) Pour tout
 ,
,
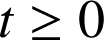 ,
, ![]() ne dépend pas de
ne dépend pas de
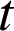 .
.
Donc 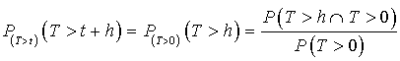 .
.
Or ![]() , d'où
, d'où 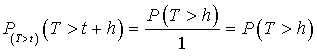 .
.
2) Montrer que : pour
 ,
,
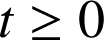 ,
, 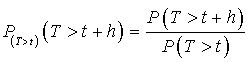 .
.
Appliquer la définition des probabilités conditionnelles.
2) Pour
 ,
,
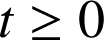 ,
,  .
.
En effet, ![]() car
car
 .
.
3) Déduire des questions 1/ et 2/ que : pour
 ,
,
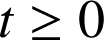 ,
, ![]() .
.
3) D'après les questions 1/ et 2/, on a, pour tout
 ,
,
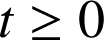 ,
, 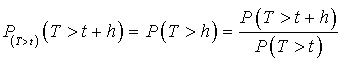 .
.
On en déduit que : ![]() .
.
4) On pose pour
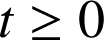 ,
, ![]() .
.
a. Vérifier que : ![]() et que, pour tout réel
et que, pour tout réel
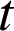 positif,
positif, ![]() .
.
b. Déduire de la question 3/ que : pour tous réels
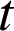 et
et
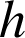 positifs,
positifs, ![]() .
.
a. Relire les données et ne pas oublier que ![]() est une probabilité.
est une probabilité.
4) a. ![]()
De plus, pour tout
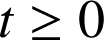 ,
, ![]() et
et
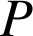 est une probabilité donc
est une probabilité donc ![]() soit
soit ![]() .
.
b. Pour
 ,
,
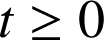 ,
, ![]() .
.
Par conséquent, ![]() .
.
1) Montrer que : pour tout entier
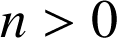 ,
, 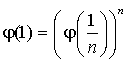 .
.
1) Appliquer plusieurs fois l'équation fonctionnelle ![]() .
.
1) Remarquer que 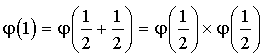 .
.
1) Pour tout entier
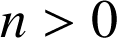 ,
, 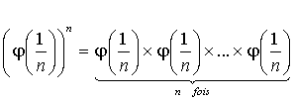 .
.
En appliquant l'égalité ![]() , on obtient
, on obtient 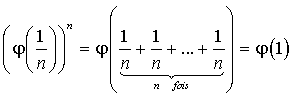 .
.
2) En déduire que : pour tout entier
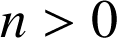 ,
, 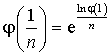 .
.
2) On pourra transformer l'égalité 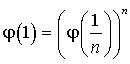 à l'aide de la fonction logarithme népérien.
à l'aide de la fonction logarithme népérien.
2) Pour tout entier
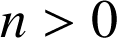 ,
, 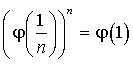 .
.
Or, pour tout réel
 ,
, ![]() , donc
, donc  .
.
D'où 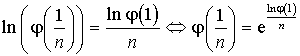 .
.
3) On pose ![]() et pour tout entier
et pour tout entier
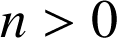 ,
, 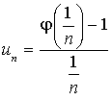 .
.
a. Vérifier que :
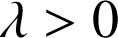 .
.
b. Vérifier que : pour tout entier
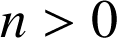 ,
,  .
.
c. En déduire que la suite ![]() converge vers
converge vers
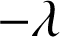 .
.
a. Démontrer en premier lieu que
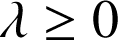 .
.
a. Justifier le fait que ![]() en utilisant la donnée du texte « il n'est pas certain que cet individu soit immortel donc il existe un entier
en utilisant la donnée du texte « il n'est pas certain que cet individu soit immortel donc il existe un entier
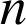 positif tel que
positif tel que ![]() ».
».
b. Un simple remplacement de 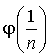 dans l'expression de
dans l'expression de
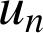 conduit au résultat.
conduit au résultat.
c. Utiliser une variable auxiliaire ![]() .
.
a. Vérifier que ![]() .
.
3) a. ![]() donc
donc ![]() et
et
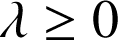 .
.
Or il existe un entier
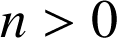 tel que
tel que ![]() , c'est-à-dire tel que
, c'est-à-dire tel que ![]() .
.
De plus ![]() , donc
, donc ![]() et
et
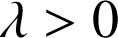 .
.
b. Pour tout entier
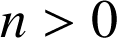 ,
, 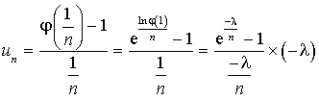 .
.
Donc pour tout entier
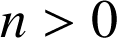 ,
, 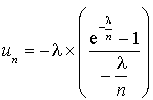 .
.
Posons ![]() , on obtient
, on obtient 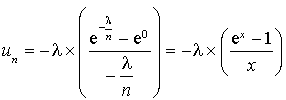 .
.
Or ![]() et
et ![]() donc
donc ![]() .
.
Étude de la dérivabilité de la fonction
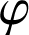
1) Montrer que la fonction
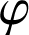 est décroissante sur
est décroissante sur ![]() .
.
Pour ![]() , comparer les événements
, comparer les événements ![]() et
et ![]() .
.
1) Soient
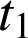 et
et
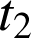 deux réels positifs tels que :
deux réels positifs tels que :
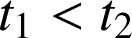 . Comparons
. Comparons ![]() et
et ![]() .
.
![]() et
et ![]() .
.
Or, comme
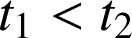 ,
, ![]() .
.
D'où ![]() et
et ![]() , par conséquent la fonction
, par conséquent la fonction
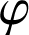 est décroissante sur
est décroissante sur ![]() .
.
2) Soit
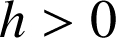 et soit
et soit
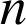 un entier strictement positif tels que :
un entier strictement positif tels que : ![]() .
.
a. Montrer que : 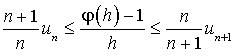 .
.
b. Montrer que la fonction
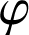 est dérivable en
est dérivable en
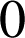 et déterminer
et déterminer
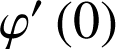 .
.
a. A partir de ![]() , appliquer la décroissance de la fonction
, appliquer la décroissance de la fonction
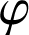 .
.
b. Revoir la définition de la dérivabilité d'une fonction en
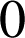 .
.
a. Montrer que : 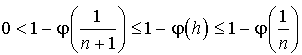 .
.
b. Revoir les théorèmes de comparaison pour calculer la limite 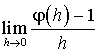 .
.
a. Ne pas oublier que ![]() .
.
2) a. ![]() , or la fonction
, or la fonction
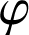 est décroissante sur
est décroissante sur ![]() .
.
D'où 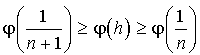 .
.
Puis 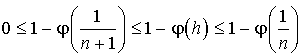 .
.
De plus ![]() , donc en multipliant membres à membres on obtient :
, donc en multipliant membres à membres on obtient : 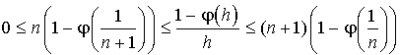 .
.
C'est-à-dire : 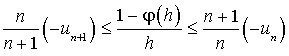 .
.
Ou encore 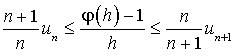 .
.
2) b. Lorsque
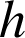 tend vers
tend vers
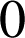 ,
,
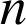 tend vers
tend vers
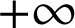 .
.
Donc ![]() et
et ![]() .
.
Or la suite ![]() converge vers
converge vers
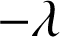 .
.
Donc ![]() et
et ![]() .
.
D'après le théorème des gendarmes, 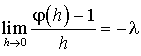 .
.
Or ![]() d'où
d'où 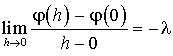 , ce qui signifie que la fonction
, ce qui signifie que la fonction
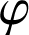 est dérivable en
est dérivable en
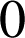 et que
et que ![]() .
.
3) a. Vérifier que : pour
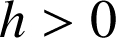 ,
,
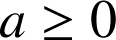 ,
, 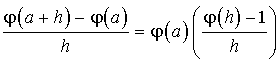 .
.
b. En déduire que la fonction
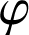 est dérivable sur
est dérivable sur ![]() .
.
c. Montrer que la fonction
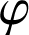 est solution de l'équation différentielle :
est solution de l'équation différentielle : ![]() .
.
d. Exprimer pour tout réel
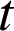 positif,
positif, ![]() en fonction de
en fonction de
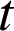 .
.
a. La fonction
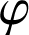 vérifie l'équation fonctionnelle
vérifie l'équation fonctionnelle ![]() .
.
b. Calculer la limite 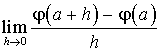 .
.
c. 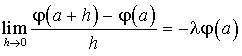
b. Revoir la définition de la dérivabilité d'une fonction en
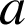 .
.
d. Revoir les équations différentielles de la forme
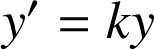 .
.
b. Or 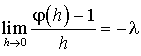 . Donc
. Donc 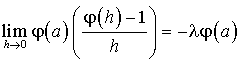 .
.
On obtient 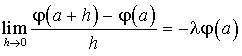 et on en déduit que la fonction
et on en déduit que la fonction
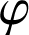 est dérivable en
est dérivable en
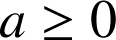 . Donc la fonction
. Donc la fonction
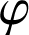 est dérivable sur
est dérivable sur ![]() .
.
c. D'après la question précédente, 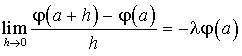 .
.
Donc, pour
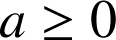 ,
, ![]() . Par conséquent la fonction
. Par conséquent la fonction
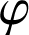 est solution de l'équation différentielle
est solution de l'équation différentielle ![]() .
.
d. Les fonctions dérivables sur ![]() solutions de l'équation différentielle
solutions de l'équation différentielle ![]() sont les fonctions définies sur
sont les fonctions définies sur ![]() par :
par : ![]() où
où
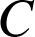 est une constante réelle. Or
est une constante réelle. Or ![]() donc
donc
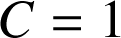 .
.
Donc pour
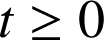 ,
, ![]() .
.
1) a. Exprimer pour tout réel
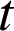 positif,
positif,![]() en fonction de
en fonction de
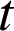 .
.
b. Vérifier que
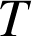 est la loi exponentielle de paramètre
est la loi exponentielle de paramètre
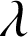 dont on précisera la fonction densité
dont on précisera la fonction densité
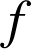 .
.
a. Quel est l'événement contraire de ![]() ?
?
b. Définition :
La loi exponentielle de paramètre
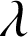 sur
sur ![]() a pour densité la fonction
a pour densité la fonction
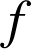 définie sur
définie sur ![]() par
par ![]() , où
, où
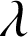 est un réel strictement positif.
est un réel strictement positif.
1) a. Pour tout réel
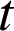 positif,
positif, ![]() .
.
b. Pour tout réel
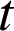 positif,
positif, ![]() avec
avec
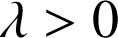 .
.
On reconnaît la définition de la loi exponentielle de paramètre
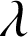 et de fonction densité
et de fonction densité
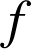 définie sur
définie sur ![]() par
par ![]() .
.
2) Pour tout réel
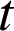 positif, on pose
positif, on pose ![]() .
.
a. Calculer
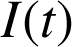 en fonction de
en fonction de
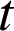 .
.
b. Déterminer ![]() en fonction de
en fonction de
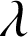 .
.
On note ![]() . Par définition, c'est l'espérance mathématique de la loi
. Par définition, c'est l'espérance mathématique de la loi
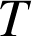 . D'où
. D'où ![]() .
.
a. Utiliser une intégration par parties.
b. Utiliser ![]() et
et ![]() .
.
a. On pourra poser ![]() et
et ![]() .
.
2) Pour tout réel
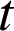 positif ? on pose
positif ? on pose ![]() .
.
a. On calcule ![]() à l'aide d'une intégration par parties.
à l'aide d'une intégration par parties.
On pose ![]() et
et ![]() donc
donc ![]() et
et ![]() .
.
![]()
![]()
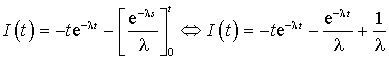 .
.
b. Or ![]() et
et ![]() donc
donc ![]() .
.







