1)
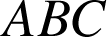 est un triangle rectangle isocèle en
est un triangle rectangle isocèle en
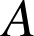 direct.
direct.
La transformation ![]() du plan est la composée de la translation
du plan est la composée de la translation
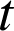 de vecteur
de vecteur ![]() et de la rotation
et de la rotation
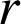 de centre
de centre
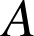 et d'angle
et d'angle ![]() .
.
Après avoir déterminé la nature de ![]() , et déterminé l'image de
, et déterminé l'image de
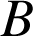 par
par ![]() , caractériser
, caractériser ![]() .
.
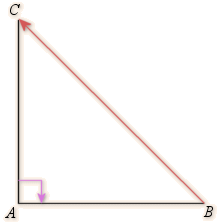
![]() est la composée de deux similitudes de rapport
est la composée de deux similitudes de rapport
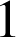 et d'angles
et d'angles ![]() pour
pour
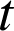 et
et ![]() pour
pour
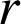 .
.
![]() est donc une similitude de rapport
est donc une similitude de rapport
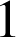 (isométrie) et d'angle
(isométrie) et d'angle ![]() , c'est une rotation.
, c'est une rotation.
![]() (
(
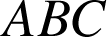 rectangle isocèle en
rectangle isocèle en
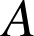 direct donc
direct donc ![]() et
et ![]() ).
).
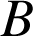 est invariant par
est invariant par ![]() c'est donc le centre de la rotation
c'est donc le centre de la rotation ![]() .
.
![]() est donc la rotation de centre
est donc la rotation de centre
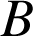 et d'angle
et d'angle ![]() .
.
La composée ![]() est aussi une rotation d'angle
est aussi une rotation d'angle ![]() ; son centre est le point
; son centre est le point
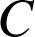
![]() ;
; ![]() .
.
2) Le plan est rapporté à un repère orthonormal ![]() ,
,
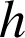 est l'homothétie de centre
est l'homothétie de centre ![]() et de rapport
et de rapport
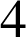 , et
, et
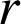 est la rotation de centre
est la rotation de centre ![]() et d'angle
et d'angle ![]() .
.
a. Après avoir justifié que ![]() est une similitude directe, déterminer son rapport et son angle.
est une similitude directe, déterminer son rapport et son angle.
b. Déterminer l'image
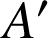 de
de
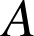 par
par
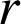 , puis en déduire l'écriture complexe de
, puis en déduire l'écriture complexe de ![]() .
.
a.
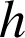 est une similitude directe de rapport
est une similitude directe de rapport
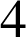 et d'angle
et d'angle ![]() et
et
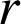 est une similitude directe de rapport
est une similitude directe de rapport
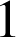 et d'angle
et d'angle ![]() donc la composée
donc la composée ![]() est une similitude directe de rapport
est une similitude directe de rapport
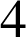 et d'angle
et d'angle ![]() .
.
b. L'image
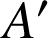 de
de
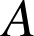 a pour affixe
a pour affixe ![]() tel que
tel que ![]() , soit
, soit ![]() d'où
d'où ![]() .
.
![]() a pour rapport
a pour rapport
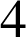 et pour angle
et pour angle ![]() , donc une écriture complexe de la forme
, donc une écriture complexe de la forme 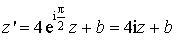 ;
; ![]() donc
donc ![]() d'où
d'où ![]() .
.
![]() a donc pour écriture complexe :
a donc pour écriture complexe : ![]() .
.






