1) Le plan est rapporté à un repère orthonormal 
, et une similitude directe
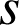a pour écriture complexe : 
.
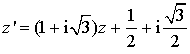Justifier que
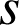peut s'écrire 
où
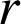est une rotation et
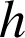une homothétie de même centre.
D'après son écriture complexe,
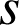a pour rapport 
et pour angle 
.
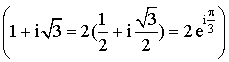L'équation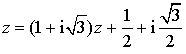 
admet pour solution 
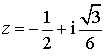donc
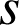admet le point 
d'affixe 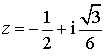pour centre ;
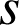admet donc pour écriture réduite 
.
2) Le plan est rapporté à un repère orthonormal et les transformations 
et 
ont respectivement pour écriture complexe : 
et 
.
a. Déterminer la nature et les éléments caractéristiques de et .
b. Déterminer la nature et les éléments caractéristique de 
. En déduire que est une homothétie.
a. L'écriture complexe de est l'écriture complexe d'une similitude directe de rapport 
, d'angle 
.
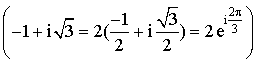admet pour élément invariant
.
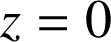est donc la similitude directe de centre
, de rapport
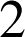et d'angle 
; 
.
L'écriture complexe de est de la forme 
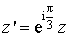, c'est donc l'écriture complexe de la rotation de centre
et d'angle 
(similitude directe de centre
, de rapport
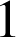et d'angle ).
b. La composée est une similitude directe de rapport
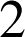(produit des rapports), d'angle 
(somme des angles) ; Le point
est invariant par , c'est donc le centre.
est donc l'homothétie de centre
et de rapport
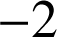. (remarquons que, dans ce cas, 
).
A l'aide des écritures complexes, a pour écriture complexe :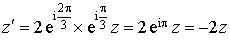 
.
On retrouve l'écriture complexe de l'homothétie de centre
et de rapport
.
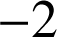