1) Une transformation
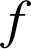du plan a pour écriture complexe 
où 
et 
.
Préciser la nature de
.
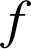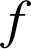a pour écriture complexe 
(propriétés du conjugué), donc l'écriture complexe de
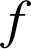est celle d'une similitude directe de rapport 
.
En particulier, si 
,
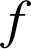est une translation.
Si
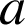réel,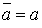 
,
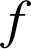est une homothétie.Si
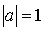et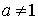 
,
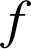est une rotation.
2) Une transformation
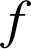du plan a pour écriture complexe 
où . Après avoir justifié que
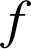est une similitude directe, déterminer :
a. L'ensemble
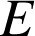des nombres complexes
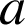tels que
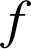est une translation.
b. L'ensemble
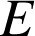des nombres complexes
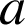tels que
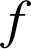est une homothétie de rapport
.
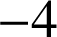c. L'ensemble
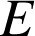des nombres complexes
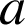tels que
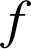est une rotation d'angle 
.
L'écriture complexe de
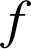est de la forme 
avec et , et donc
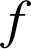est une similitude directe de rapport 
.
a.
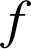est une translation si et seulement si 
.
ou 
b.
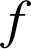est une homothétie de rapport
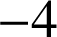si et seulement si
.
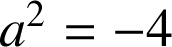ou 
c.
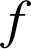est une rotation d'angle si et seulement si 
.
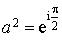Si
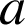a pour module 
et pour argument 
,
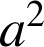a pour module 
et pour argument 
d'où :
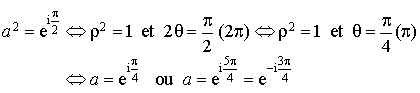
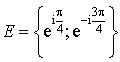
3) Une similitude directe
du plan muni d'un repère orthonormal direct 
, vérifie 
et 
où les points
,
,
,
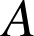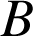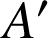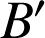ont pour affixes respectives
,
,
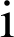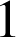, et
.
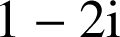Déterminer une écriture complexe de
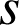; préciser le rapport de
.
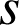étant une similitude directe, elle admet une écriture complexe de la forme où et .
et donc
est solution du système :
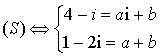
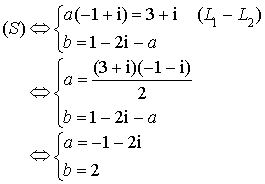
admet donc pour écriture complexe 
;
a pour rapport 
.
