Si
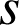 est une similitude directe alors il existe un réel
est une similitude directe alors il existe un réel ![]() tel que, pour tous points
tel que, pour tous points
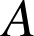 et
et
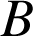 d'images respectives
d'images respectives
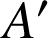 et
et
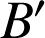 :
: ![]() .
.
Ce réel ![]() est appelé angle de la similitude directe
est appelé angle de la similitude directe
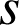 .
.
Si l'écriture complexe de
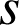 est
est ![]() alors
alors ![]()
![]() .
.
Si
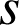 est de rapport
est de rapport
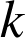 et d'angle
et d'angle ![]() alors pour tous points
alors pour tous points
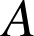 et
et
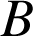 d'images respectives
d'images respectives
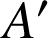 et
et
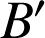 alors
alors ![]() et
et ![]() .
.
Pour une translation,
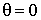
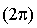 .
.Pour une homothétie,
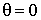
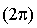 si le rapport de l'homothétie est positif.
si le rapport de l'homothétie est positif. 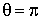
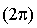 si le rapport de l'homothétie est négatif.
si le rapport de l'homothétie est négatif.Pour une rotation,
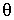 est l'angle de la rotation.
est l'angle de la rotation.Pour la similitude réciproque
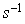 , l'angle est égal à
, l'angle est égal à 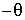
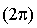 .
.Pour la composée
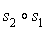 de deux similitudes directes d'angles respectifs
de deux similitudes directes d'angles respectifs 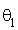 et
et 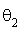 , l'angle est égal à
, l'angle est égal à 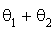
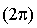 .
.
La composée d'une rotation d'angle
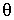 et d'une homothétie de rapport
et d'une homothétie de rapport
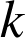 est une similitude directe de rapport
est une similitude directe de rapport 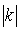 et d'angle
et d'angle 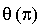 .
.La composée de deux homothéties de rapport
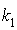 et
et 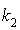 est une similitude directe de rapport
est une similitude directe de rapport 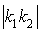 et d'angle
et d'angle 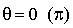 , c'est une translation (
, c'est une translation (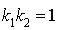 ) ou une homothétie.
) ou une homothétie.La composée de deux rotations d'angles
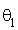 et
et 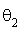 est une similitude directe de rapport
est une similitude directe de rapport
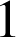 (donc une isométrie) et d'angle
(donc une isométrie) et d'angle 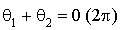 ou
ou 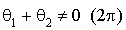 ; c'est une translation ou une rotation.
; c'est une translation ou une rotation.La composée d'une translation et d'une rotation d'angle
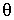 est une similitude directe de rapport
est une similitude directe de rapport
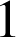 (donc une isométrie), d'angle
(donc une isométrie), d'angle 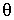 ; c'est une rotation d'angle
; c'est une rotation d'angle 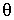 .
.






