1) Soit ![]() un segment,
un segment, ![]() la rotation de centre
la rotation de centre
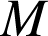 et d'angle
et d'angle ![]() ,
, ![]() la rotation de centre
la rotation de centre
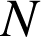 et d'angle
et d'angle ![]() .
.
Après avoir déterminé la nature de ![]() , et déterminé l'image de
, et déterminé l'image de
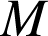 par
par ![]() , caractériser
, caractériser ![]() .
.
![]() est la composée de deux déplacements d'angle
est la composée de deux déplacements d'angle ![]() , c'est donc un déplacement d'angle
, c'est donc un déplacement d'angle ![]() ; c'est donc une rotation d'angle
; c'est donc une rotation d'angle ![]() ou encore une symétrie centrale.
ou encore une symétrie centrale.
![]() avec
avec
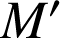 tel que
tel que ![]() et
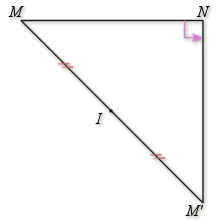
et ![]() ; le triangle
; le triangle
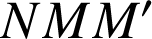 est rectangle isocèle direct en
est rectangle isocèle direct en
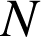 .
.
![]() donc le centre de
donc le centre de ![]() est le milieu
est le milieu
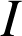 de
de ![]() .
.
![]() est aussi une rotation d'angle
est aussi une rotation d'angle ![]() , donc une symétrie centrale ; l'image de
, donc une symétrie centrale ; l'image de
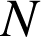 par
par ![]() est le point
est le point
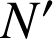 tel
tel
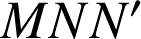 rectangle isocèle direct en
rectangle isocèle direct en
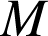 ;le quadrilatère
;le quadrilatère
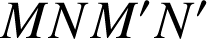 est un carré d'où le centre de
est un carré d'où le centre de ![]() est le même que celui de
est le même que celui de ![]() d'où
d'où ![]() =
= ![]() .
.
2) Soit
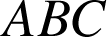 et
et
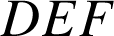 deux triangles équilatéraux directs,
deux triangles équilatéraux directs, ![]() .
.
Les points
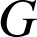 et
et
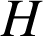 sont tels que
sont tels que
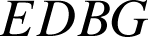 et
et
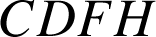 soient des parallélogrammes. Le but de l'exercice est de démontrer que le triangle
soient des parallélogrammes. Le but de l'exercice est de démontrer que le triangle
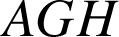 est équilatéral.
est équilatéral.
Soit ![]() , où
, où ![]() est la translation de vecteur
est la translation de vecteur ![]() ,
, ![]() la translation de vecteur
la translation de vecteur ![]() et
et
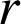 la rotation de centre
la rotation de centre
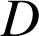 et d'angle
et d'angle ![]() .
.
a. Déterminer ![]() puis la nature et les éléments caractéristiques de
puis la nature et les éléments caractéristiques de
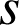 .
.
b. Déterminer l'image de
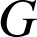 par
par
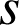 ; en déduire que le triangle
; en déduire que le triangle
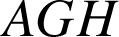 est équilatéral.
est équilatéral.
a. ![]() ;
;
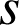 est la composée de 3 déplacements, c'est donc un déplacement,
est la composée de 3 déplacements, c'est donc un déplacement,
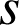 est une similitude directe d'angle
est une similitude directe d'angle ![]() , c'est donc une rotation d'angle
, c'est donc une rotation d'angle ![]() .
.
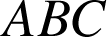 est un triangle équilatéral direct d'où
est un triangle équilatéral direct d'où 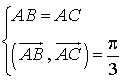 ;
;
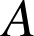 est donc le centre de la rotation
est donc le centre de la rotation ![]() .
.
b. ![]() (
(
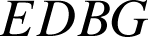 parallélogramme) donc
parallélogramme) donc ![]() ;
;
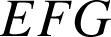 équilatéral donc
équilatéral donc ![]() ;
;
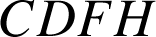 parallélogramme donc
parallélogramme donc ![]() .
.
![]() donc
donc 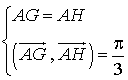 ; le triangle
; le triangle
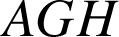 est équilatéral.
est équilatéral.






