Introduction
Durée :30 minutes
Niveau : moyen
Déterminer une primitive des fonctions
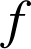 et
et
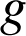 sur l'intervalle
sur l'intervalle
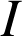 indiqué :
indiqué :
Durée :30 minutes
Niveau : moyen
Déterminer une primitive des fonctions
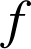 et
et
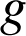 sur l'intervalle
sur l'intervalle
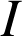 indiqué :
indiqué :