Introduction
Durée : 30 minutes
Niveau : moyen
Sans aucun calcul, donner le signe de chacune des intégrales suivantes :
Signe de l'intégrale :
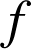 est une fonction continue sur un intervalle
est une fonction continue sur un intervalle
 ,
,
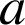 et
et
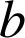 deux éléments de
deux éléments de
 tels que
tels que ![]() .
.
si
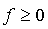 sur
sur
 , alors :
, alors : 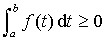 ,
,si
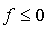 sur
sur
 , alors :
, alors : 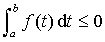 .
.
1) ![]()
La fonction
 définie par
définie par ![]() est continue et positive sur
est continue et positive sur
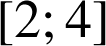 donc l'intégrale
donc l'intégrale ![]() est positive.
est positive.
2) 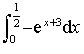
La fonction
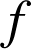 définie par
définie par ![]() est continue et négative sur
est continue et négative sur 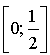 , donc l'intégrale
, donc l'intégrale 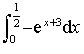 est négative.
est négative.
3) ![]()
![]() . Or la fonction
. Or la fonction
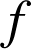 définie par
définie par ![]() est continue et positive sur
est continue et positive sur ![]() , donc l'intégrale
, donc l'intégrale ![]() est positive et
est positive et ![]() est négative.
est négative.
4) ![]()
![]() . Or la fonction
. Or la fonction
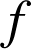 définie par
définie par ![]() est continue et négative sur
est continue et négative sur
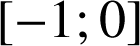 , donc l'intégrale
, donc l'intégrale ![]() est négative et
est négative et ![]() est positive.
est positive.
Comparaison d'intégrales
Comparaison d'intégrales :
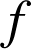 et
et
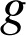 sont deux fonctions continues sur un intervalle
sont deux fonctions continues sur un intervalle
 ,
,
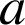 et
et
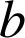 deux éléments de
deux éléments de
 tels que
tels que ![]() .
.
Si ![]() pour tout
pour tout
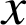 appartenant à
appartenant à
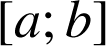 , alors :
, alors : ![]() .
.
1) Montrer que pour tout réel
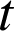 de
de
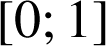 :
: ![]() .
.
![]() donc
donc ![]() et
et ![]() .
.
Comme ![]() ,
, ![]() .
.
2) En déduire un encadrement de l'intégrale ![]() .
.
En intégrant sur
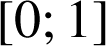 ,
, ![]() .
.
Donc 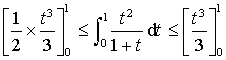 et
et ![]() .
.






