Introduction
Durée : 20 minutes
Niveau : moyen
Déterminer la valeur moyenne de chacune des fonctions suivantes sur l'intervalle considéré :
Linéarité :
Soient
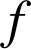et
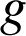deux fonctions continues sur un intervalle
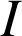. Soit
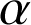un réel quelconque,
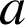et
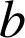deux éléments de
.
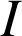1) 
sur
.
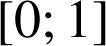car 
.
2) 
sur
.
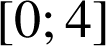Par linéarité de l'intégrale : 
.
Or et 
donc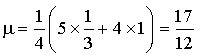 
.
On considère les intégrales 
, 
et 
.
Linéarité :
Soient
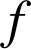et
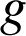deux fonctions continues sur un intervalle
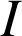. Soit
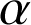un réel quelconque,
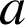et
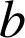deux éléments de
.
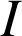Calculer
.
Exprimer
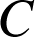en fonction de
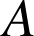et
.
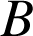On admet que
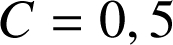. En déduire les valeurs de
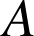et
.
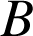Or 
donc 
.
De plus,
Donc 
par conséquent
.
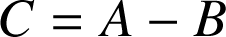Comme
,
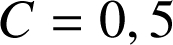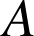et
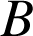sont solutions du système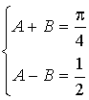 
On obtien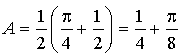t 
et 
.
