Introduction
Durée :50 minutes
Niveau : moyen
Soit
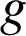 une fonction définie et dérivable, de dérivée
une fonction définie et dérivable, de dérivée
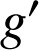 continue sur
continue sur
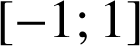 .
.
La courbe représentative de
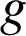 est donnée ci-dessous :
est donnée ci-dessous :
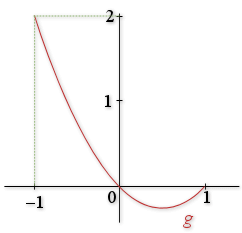
Les affirmations suivantes sont-elles cohérentes avec le schéma ?
Théorème fondamental du calcul intégral :
Soient
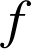 une fonction continue sur un intervalle
une fonction continue sur un intervalle
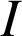 ,
,
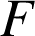 une primitive de
une primitive de
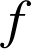 sur
sur
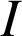 et
et
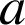 et
et
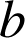 deux réels de
deux réels de
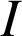 .
. ![]() .
.
On note aussi : ![]() .
.
Comparaison d'intégrales :
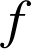 et
et
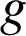 sont deux fonctions continues sur un intervalle
sont deux fonctions continues sur un intervalle
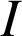 ,
,
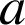 et
et
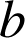 deux éléments de
deux éléments de
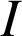 tels que
tels que ![]() .
.
Si ![]() , pour tout
, pour tout
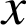 appartenant à
appartenant à
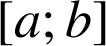 , alors :
, alors : ![]() .
.
1) ![]()
Par hypothèses
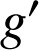 est continue sur
est continue sur
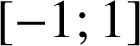 donc
donc ![]() .
.
Or
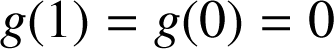 donc
donc ![]() .
.
L'affirmation est donc cohérente avec le graphique.
2) ![]()
D'après le graphique, la fonction g est minorée par ![]() .
.
Donc, pour tout réel
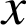 de
de
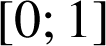 ,
, ![]() .
.
Comme
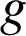 est une fonction dérivable sur
est une fonction dérivable sur
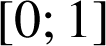 , on peut intégrer cette inégalité sur
, on peut intégrer cette inégalité sur
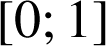 , on obtient :
, on obtient : ![]() .
.
On en déduit que ![]() .
.
L'affirmation est donc cohérente avec le graphique.
Calculer la valeur moyenne de ![]() sur
sur ![]() .
.
Théorème fondamental du calcul intégral :
Soient
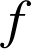 une fonction continue sur un intervalle
une fonction continue sur un intervalle
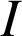 ,
,
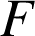 une primitive de
une primitive de
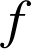 sur
sur
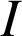 et
et
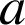 et
et
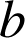 deux réels de
deux réels de
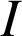 .
. ![]() .
.
On note aussi : ![]() .
.
La fonction ![]() est continue sur
est continue sur ![]() , donc la valeur moyenne de la fonction
, donc la valeur moyenne de la fonction ![]() sur
sur ![]() est :
est : 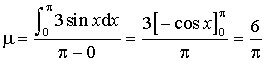 .
.
Soit la fonction
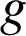 définie sur
définie sur
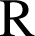 par :
par : ![]() .
.
Théorème fondamental du calcul intégral :
Soient
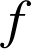 une fonction continue sur un intervalle
une fonction continue sur un intervalle
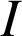 ,
,
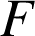 une primitive de
une primitive de
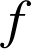 sur
sur
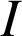 et
et
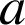 et
et
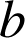 deux réels de
deux réels de
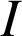 .
. ![]() .
.
On note aussi : ![]() .
.
1) a. Justifier que
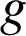 est dérivable sur
est dérivable sur
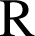 et déterminer sa dérivée
et déterminer sa dérivée
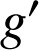 .
.
b. Justifier que
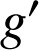 est dérivable sur
est dérivable sur
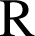 et déterminer sa dérivée
et déterminer sa dérivée
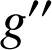 .
.
a. Les fonctions ![]() et
et ![]() sont dérivables sur
sont dérivables sur
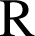 donc, par produit,
donc, par produit,
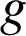 est dérivable sur
est dérivable sur
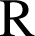 . Pour tout réel
. Pour tout réel
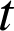 ,
,
b. Les fonctions ![]() et
et ![]() sont dérivables sur
sont dérivables sur
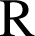 donc, par produit,
donc, par produit,
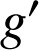 est dérivable sur
est dérivable sur
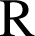 . Pour tout réel
. Pour tout réel
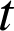 ,
,
2) a. Vérifier que pour tout
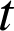 de
de
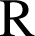 :
: ![]() .
.
b. En déduire une primitive
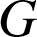 de
de
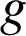 sur
sur
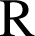 .
.
c. Calculer l'intégrale 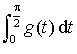 .
.
a. Pour tout
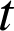 de
de
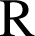 ,
, ![]()
Donc, pour tout
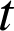 de R,
de R, ![]() .
.
b. La fonction
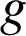 est dérivable sur R, elle y admet des primitives et l'une d'entre elles est la fonction
est dérivable sur R, elle y admet des primitives et l'une d'entre elles est la fonction
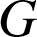 définie sur
définie sur
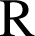 par
par ![]() .
.
Donc, pour tout
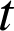 de R,
de R, ![]() .
.
![]()
c. 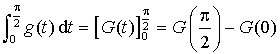
et 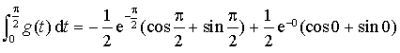
D'où 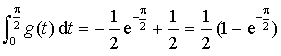 .
.






