Introduction
Durée : 30 minutes
Niveau : moyen
Déterminer par des considérations d'aires, de parité ou de périodicité les intégrales suivantes :
Parité et périodicité :
Si
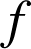 est continue sur
est continue sur
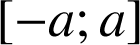 et paire alors
et paire alors ![]() .
.
Si
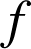 est continue sur
est continue sur
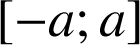 et impaire alors
et impaire alors ![]() .
.
Si
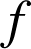 est périodique de période
est périodique de période
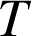 et continue sur les intervalles
et continue sur les intervalles
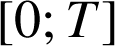 et
et
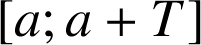 alors
alors ![]() .
.
1) ![]()
![]()
Donc | 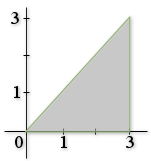 |
Par conséquent ![]() .
.
2) ![]()
La fonction valeur absolue est paire donc ![]() .
.
3) ![]()
La fonction
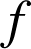 définie sur
définie sur
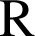 par
par
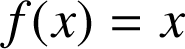 est impaire donc
est impaire donc ![]() .
.
4) 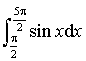
La fonction sinus est périodique de période
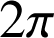 .
.
Or l'intervalle 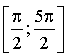 a pour amplitude
a pour amplitude
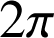 donc
donc 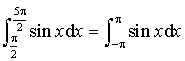 .
.
De plus la fonction sinus est impaire donc 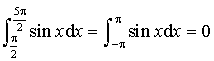 .
.
Proposer une fonction polynôme
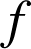 de degré supérieur ou égal à
de degré supérieur ou égal à
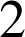 dont la valeur moyenne sur
dont la valeur moyenne sur
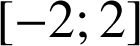 est égale à
est égale à
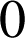 .
.
Valeur moyenne d'une fonction continue :
Soit
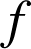 une fonction continue sur l'intervalle
une fonction continue sur l'intervalle
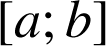 avec
avec
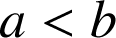 .
.
On appelle valeur moyenne de
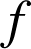 sur
sur
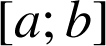 , le réel
, le réel ![]() .
.
On cherche une fonction
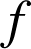 continue sur
continue sur
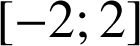 telle que :
telle que : 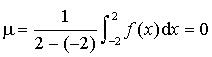 , c'est-à-dire telle que
, c'est-à-dire telle que ![]() .
.
Il suffit de choisir
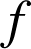 fonction polynôme de degré supérieur ou égal à
fonction polynôme de degré supérieur ou égal à
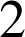 et impaire par exemple :
et impaire par exemple :
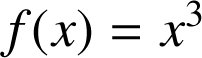 .
.






