Introduction
Durée :30 minutes
Niveau : moyen
1. En écrivant l'intégrale ![]() , utiliser une intégration par parties pour calculer pour
, utiliser une intégration par parties pour calculer pour
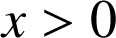 , l'intégrale
, l'intégrale ![]() .
.
Intégration par parties :
Soient
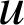 et
et
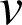 deux fonctions dérivables sur
deux fonctions dérivables sur
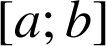 et admettant des dérivées continues sur
et admettant des dérivées continues sur
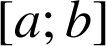 . On a alors :
. On a alors :
Théorème :
Soit
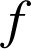 une fonction continue sur un intervalle
une fonction continue sur un intervalle
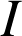 et
et
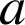 un réel appartenant à
un réel appartenant à
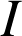 .
.
La fonction ![]() est la primitive de
est la primitive de
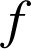 sur
sur
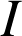 qui s'annule en
qui s'annule en
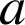 .
.
Soient les fonctions
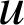 et
et
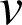 définies sur
définies sur
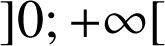 par
par ![]() et
et
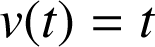 .
.
Les fonctions
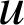 et
et
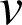 sont dérivables sur
sont dérivables sur
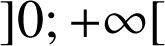 et les fonctions
et les fonctions
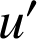 et
et
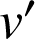 sont continues sur
sont continues sur
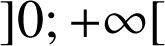 .
.
En appliquant la formule d'intégration par parties, on obtient pour
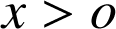 :
:
![]() et
et ![]() .
.
Donc pour
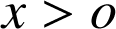 ,
, ![]() .
.
2. En déduire une primitive de la fonction
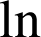 sur
sur
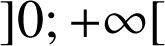 .
.
La fonction
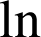 étant continue sur
étant continue sur
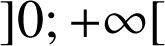 , la fonction
, la fonction
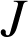 définie sur
définie sur
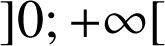 par
par ![]() est par définition la primitive de la fonction
est par définition la primitive de la fonction
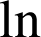 s'annulant en
s'annulant en
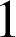 .
.
A l'aide d'une double intégration par parties, calculer ![]() .
.
Intégration par parties :
Soient
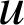 et
et
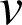 deux fonctions dérivables sur
deux fonctions dérivables sur
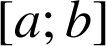 et admettant des dérivées continues sur
et admettant des dérivées continues sur
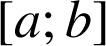 . On a alors :
. On a alors :
Soient les fonctions
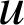 et
et
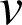 définies sur
définies sur
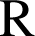 par
par
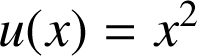 et
et
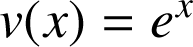 .
.
Les fonctions
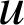 et
et
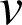 sont dérivables sur
sont dérivables sur
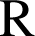 et les fonctions
et les fonctions
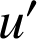 et
et
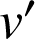 sont continues sur
sont continues sur
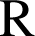 .
.
En appliquant la formule d'intégration par parties, on obtient :
On pose ![]() .
.
Soient les fonctions
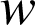 et
et
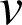 définies sur
définies sur
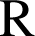 par
par
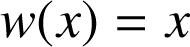 et
et
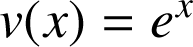 .
.
Les fonctions
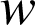 et
et
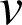 sont dérivables sur
sont dérivables sur
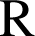 et les fonctions
et les fonctions
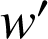 et
et
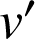 sont continues sur
sont continues sur
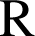 .
.
En appliquant la formule d'intégration par parties, on obtient :
D'où ![]() .
.






