Introduction
Durée : 45 minutes
Niveau : moyen
On pose ![]() avec
avec ![]() .
.
Inégalité de la moyenne :
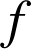 est une fonction continue sur un intervalle
est une fonction continue sur un intervalle
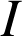 ,
,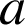 et
et
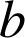 deux éléments de
deux éléments de
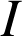 tels que
tels que 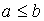 ,
,
 et
et
 sont deux réels.
sont deux réels.
Si pour tout
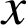 de
de
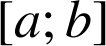 ,
, ![]() , alors
, alors ![]() .
.
1) Étudier les variations de la fonction
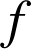 sur
sur
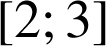 .
.
 est dérivable sur
est dérivable sur
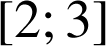 et pour tout réel
et pour tout réel
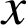 de
de
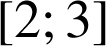 .
.
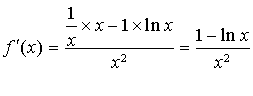 .
.
Or sur
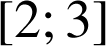 ,
,
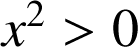 donc le signe de
donc le signe de
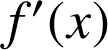 ne dépend que de celui de
ne dépend que de celui de ![]() .
.
En utilisant la stricte croissance de la fonction
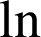 sur
sur
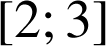 , on obtient :
, on obtient :
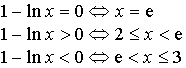
On en déduit que la fonction
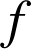 est strictement croissante sur
est strictement croissante sur
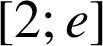 et strictement décroissante sur
et strictement décroissante sur
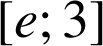 ; d'où le tableau de variations de
; d'où le tableau de variations de
 .
.
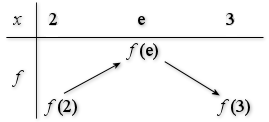
2) En déduire un encadrement d'amplitude
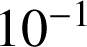 de
de
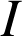 .
.
D'après la question précédente, pour tout réel
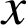 de
de
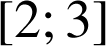 ,
, ![]() .
.
Or ![]() ,
, ![]() et
et ![]() .
.
Donc pour tout réel
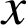 de
de
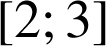 ,
, ![]() .
.
La fonction
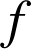 est continue sur
est continue sur
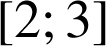 . D'après l'inégalité de la moyenne, on obtient
. D'après l'inégalité de la moyenne, on obtient ![]() .
.
Soit
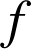 une fonction continue sur
une fonction continue sur
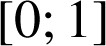 , telle que, pour tout
, telle que, pour tout
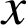 de
de
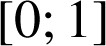 ,
, ![]() .
.
Déterminer la limite de la suite de terme général 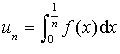 avec
avec
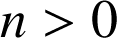 .
.
Inégalité de la moyenne :
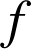 est une fonction continue sur un intervalle
est une fonction continue sur un intervalle
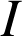 ,
,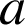 et
et
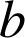 deux éléments de
deux éléments de
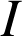 tels que
tels que 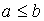 ,
,
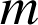 et
et
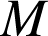 sont deux réels.
sont deux réels.
Si pour tout
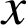 de
de
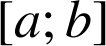 ,
, ![]() , alors
, alors ![]() .
.
Pour tout
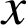 de
de
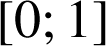 ,
, ![]() .
.
Comme
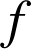 est une fonction continue sur
est une fonction continue sur 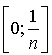 , d'après l'inégalité de la moyenne, on obtient :
, d'après l'inégalité de la moyenne, on obtient : 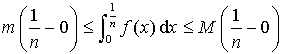 et
et ![]() .
.
Or ![]() donc, d'après le théorème des gendarmes,
donc, d'après le théorème des gendarmes, ![]() .
.
Soit
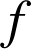 une fonction continue, monotone sur
une fonction continue, monotone sur
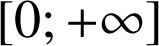 , et vérifiant :
, et vérifiant : ![]() (où
(où
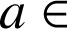 R ).
R ).
On pose pour ![]() ,
, ![]() .
.
Inégalité de la moyenne :
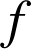 est une fonction continue sur un intervalle
est une fonction continue sur un intervalle
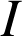 ,
,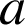 et
et
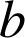 deux éléments de
deux éléments de
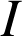 tels que
tels que 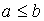 ,
,
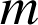 et
et
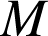 sont deux réels.
sont deux réels.
Si pour tout
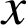 de
de
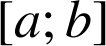 ,
, ![]() , alors
, alors ![]() .
.
1) Montrer que : pour ![]() ,
,
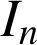 est compris entre
est compris entre
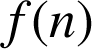 et
et
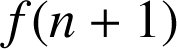 .
.
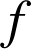 est une fonction monotone sur
est une fonction monotone sur
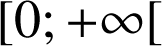 :
:
soit
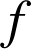 est une fonction croissante sur
est une fonction croissante sur
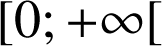 :
:Dans ce cas, si
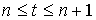 , alors
, alors 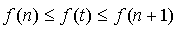 .
.Comme
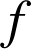 est continue sur
est continue sur
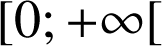 , en intégrant sur
, en intégrant sur
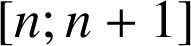 , on a :
, on a :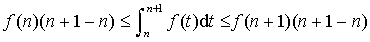
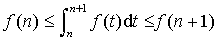 et
et 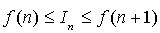
soit
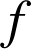 est une fonction décroissante sur
est une fonction décroissante sur
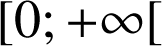 :
:Dans ce cas, si
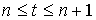 , alors
, alors 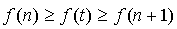 .
.Comme
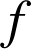 est continue sur
est continue sur
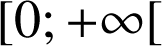 , en intégrant sur
, en intégrant sur
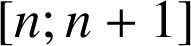 , on a :
, on a :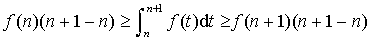
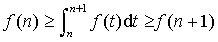 et
et 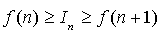
Dans les deux cas
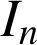 est compris entre
est compris entre
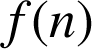 et
et
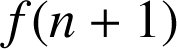 .
.
2) En déduire que ![]() .
.
On sait que ![]() donc
donc ![]() et
et ![]() .
.
D'après le théorème des gendarmes, ![]() .
.






