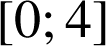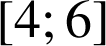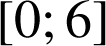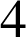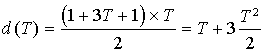Introduction
Durée : 45 minutes
Niveau : moyen
Les fonctions
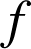 et
et
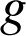 sont définies sur
sont définies sur
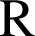 par :
par : ![]() et
et ![]() .
.
Les représentations graphiques des fonctions
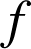 et
et
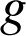 sont données ci-dessous :
sont données ci-dessous :
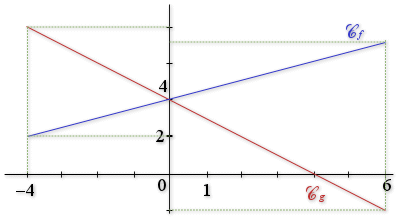
En utilisant des calculs d'aires, calculer les intégrales suivantes :
Définition :
Soit
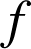 une fonction continue et positive sur un intervalle
une fonction continue et positive sur un intervalle
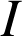 ,
, ![]() sa courbe représentative dans un repère orthogonal,
sa courbe représentative dans un repère orthogonal,
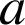 et
et
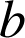 deux éléments de
deux éléments de
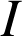 tels que
tels que ![]() . Soit
. Soit
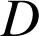 la partie du plan délimitée par la courbe
la partie du plan délimitée par la courbe ![]() , l'axe des abscisses et les droites d'équations respectives
, l'axe des abscisses et les droites d'équations respectives
 et
et
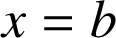 .
.
L'aire, en unités d'aire, de
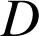 , est appelée intégrale de
, est appelée intégrale de
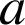 à
à
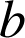 de
de
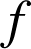 .
.
Cette intégrale se note ![]() .
.
1) ![]()
Sur
Donc | 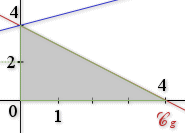 |
2) ![]()
Sur
Donc | 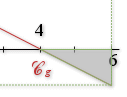 |
3) ![]()
Donc on en déduit que : ![]() .
.
4) ![]()
Sur
Donc | 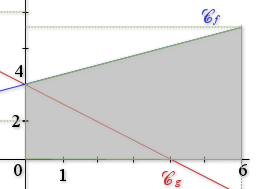 |
Un point mobile
 , situé au point
, situé au point
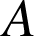 à l'instant
à l'instant
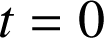 se déplace sur un segment
se déplace sur un segment
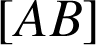 .
.
A l'instant
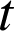 (exprimé en secondes), sa vitesse
(exprimé en secondes), sa vitesse
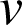 (exprimée en
(exprimée en
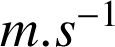 ) est donnée par :
) est donnée par :
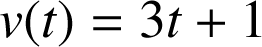 pour
pour
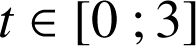 .
.
A l'instant
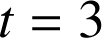 , le mobile arrive au point
, le mobile arrive au point
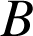 .
.
Définition :
Soit
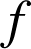 une fonction continue et positive sur un intervalle
une fonction continue et positive sur un intervalle
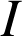 ,
, ![]() sa courbe représentative dans un repère orthogonal,
sa courbe représentative dans un repère orthogonal,
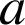 et
et
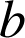 deux éléments de
deux éléments de
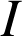 tels que
tels que ![]() . Soit
. Soit
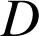 la partie du plan délimitée par la courbe
la partie du plan délimitée par la courbe ![]() , l'axe des abscisses et les droites d'équations respectives
, l'axe des abscisses et les droites d'équations respectives
 et
et
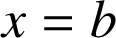 .
.
L'aire, en unités d'aire, de
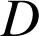 , est appelée intégrale de
, est appelée intégrale de
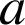 à
à
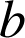 de
de
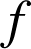 .
.
Cette intégrale se note ![]() .
.
Valeur moyenne d'une fonction continue :
Soit
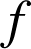 une fonction continue sur l'intervalle
une fonction continue sur l'intervalle
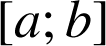 avec
avec
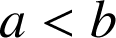 .
.
On appelle valeur moyenne de
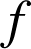 sur
sur
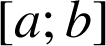 , le réel
, le réel ![]() .
.
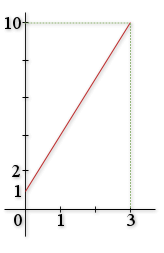
1) Représenter la vitesse du mobile en fonction du temps.
2) a. Durant une période de temps très courte, notée ![]() , on peut considérer que la vitesse
, on peut considérer que la vitesse
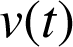 ne varie pas. Quelle est la distance
ne varie pas. Quelle est la distance
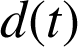 parcourue par le mobile durant cette période ?
parcourue par le mobile durant cette période ?
b. Exprimer la distance parcourue en mètres
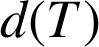 entre les instants
entre les instants
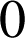 et
et
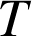 à l'aide d'une intégrale lorsque
à l'aide d'une intégrale lorsque
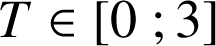 .
.
c. Visualiser sur le graphique une aire correspondant à cette intégrale et exprimer
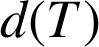 en fonction de
en fonction de
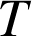 . Quel lien observe-t-on entre les fonctions
. Quel lien observe-t-on entre les fonctions
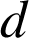 et
et
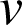 ?
?
d. Calculer la distance parcourue en mètres entre les instants
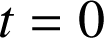 et
et
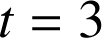 .
.
a. ![]()
b. ![]()
c.
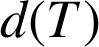 est égale à l'aire du trapèze délimité par la courbe de la fonction
est égale à l'aire du trapèze délimité par la courbe de la fonction
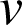 , l'axe des abscisses et les droites d'équation
, l'axe des abscisses et les droites d'équation
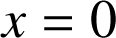 et
et
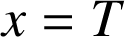 .
.
| 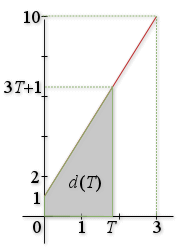 |
On peut remarquer que pour
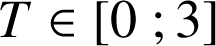 ,
,
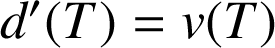 .
.
Donc la fonction
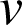 est la dérivée de la fonction
est la dérivée de la fonction
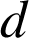 par rapport à la variable
par rapport à la variable
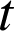 .
.
d. ![]() ; la distance parcourue est
; la distance parcourue est
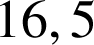 m.
m.
3) Exprimer à l'aide d'une intégrale la vitesse moyenne
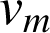 du mobile au cours de la même durée, puis la calculer.
du mobile au cours de la même durée, puis la calculer.
Par définition, 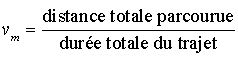 donc
donc 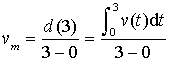 .
.
Par conséquent, ![]() , la vitesse moyenne est donc de
, la vitesse moyenne est donc de
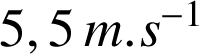 .
.