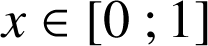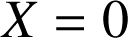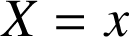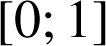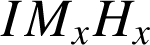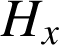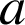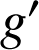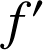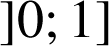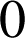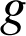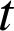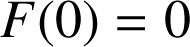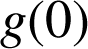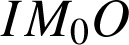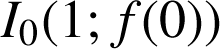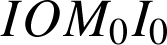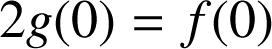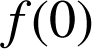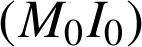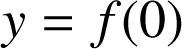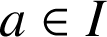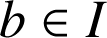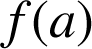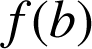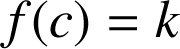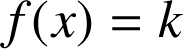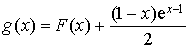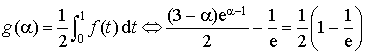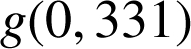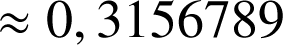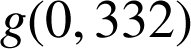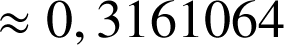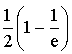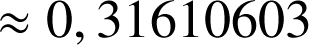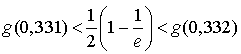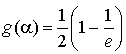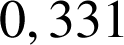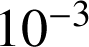Introduction
Durée : 60 minutes
Niveau : difficile
Le plan est rapporté à un repère orthonormal 
.
On note
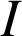le point de coordonnées
.
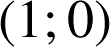Soient
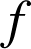une fonction positive, strictement croissante et dérivable sur
, 
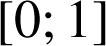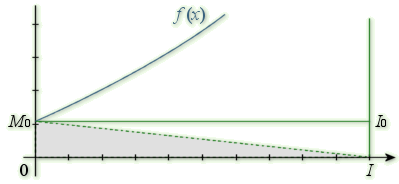
sa courbe représentative dans le repère et
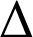la portion de plan comprise entre , l'axe des abscisses et les droites d'équations
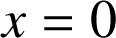et
.
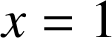Le but du problème est de prouver l'existence d'un unique réel 
appartenant à l'intervalle
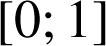tel que, si
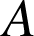est le point d'abscisse
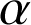, le segment
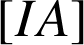partage
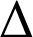en deux régions de même aire.
Pour tout
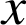appartenant à l'intervalle
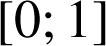; on note
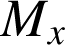le point de coordonnées
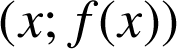et
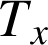le domaine délimité par la droite
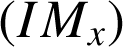, l'axe des abscisses, l'axe des ordonnées et la courbe .
On désigne par
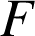la fonction définie sur
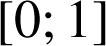par 
et
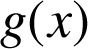l'aire de
.
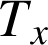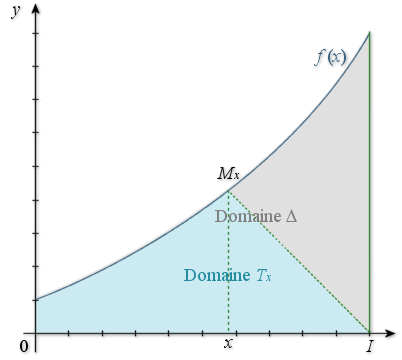
1) Exprimer, pour tout
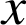appartenant à l'intervalle
,
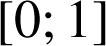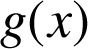en fonction de
,
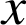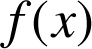et
.
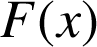2) Etudier les variations de la fonction 
sur
.
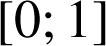3) Par des considérations d'aires ou de comparaison d'intégrales, montrer que : 
.
4) Montrer qu'il existe un unique réel
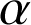de
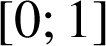tel que
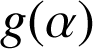soit égal à la moitié de l'aire de
.
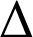5) Sachant que :
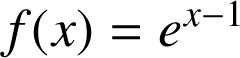; trouver une valeur approchée de
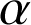à 10-3 près par défaut.
