Introduction
Durée : 50 minutes
Niveau : facile
Objectif : Calculer l'aire
et représenté ci-contre : |  |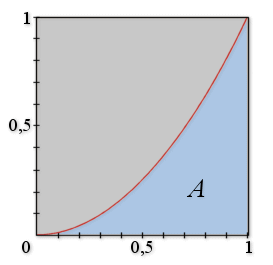
Le principe :
Soit
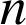un entier (
). On partage le segment
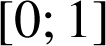en
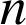segments de longueur 
.
On désigne par :
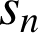la somme des aires des rectangles situés au-dessous de la courbe (en gris sur la figure ci-dessous),
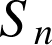la somme des aires des rectangles situés au-dessus de la courbe (en gris et blanc sur la figure ci-dessous).
Par des considérations géométriques, on en déduit que : pour , 
.
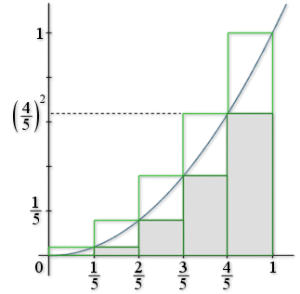 Figure pour n = 5 | Calculer
En déduire que : |
Pour
:
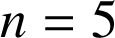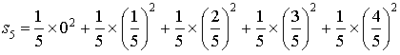
d'où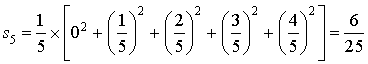 
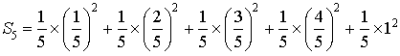
d'où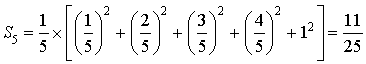 
On a 
, soit 
.
Calcul de
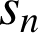et de
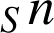
1) a. Vérifier que pour : 
.
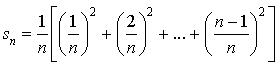On peut aussi écrire
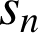sous la forme 
.
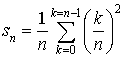b. Vérifier que pour : 
.
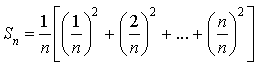On peut aussi écrire
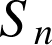sous la forme 
.
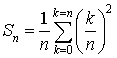Pour :
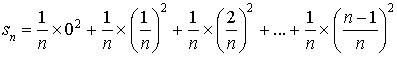
d'où
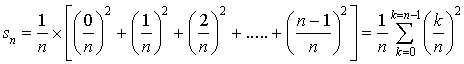
De même
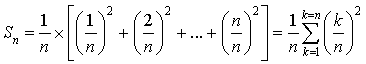
3) On rappelle que la somme des
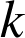premiers carrés d'entiers est :
En déduire que pour :
et 
.
On sait que pour tout
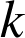entier naturel supérieur ou égal à
, 
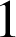(démonstration par récurrence).
On obtient donc ici :
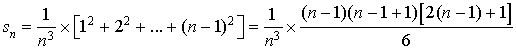
d'où 
De même :
Étude des suites
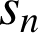et
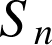
1) Démontrer que les suites
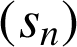et
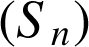sont adjacentes.
Piste : on pourra étudier le sens de variations de fonctions bien choisies.
Pour démontrer que les suites
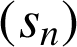et
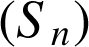sont adjacentes, il faut prouver que :
-
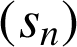est croissante et
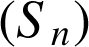décroissante,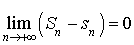
Montrons que
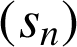est croissante.
Nous allons étudier la fonction
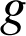définie sur
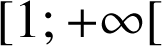par 
, car pour tout , 
.
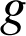est dérivable sur
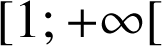comme fonction rationnelle.
Pour tout 
, 
. 
pour tout 
, d'où la fonction
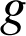est croissante sur
.
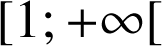On peut donc écrire : pour tout
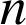tel que 
, 
, soit 
. La suite
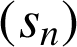est donc croissante.
On montre de même que la suite
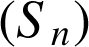est décroissante en étudiant les variations de la fonction
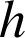définie sur
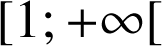par 
.
pour tout , donc
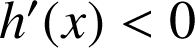pour tout et
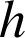est décroissante sur
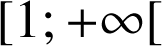. D'où
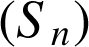est décroissante.
On a 
, donc .
Les suites
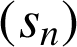et
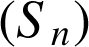sont donc adjacentes.
2) Déterminer leur limite commune
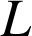et en déduire la valeur de
.
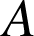Bilan :
On pose
;
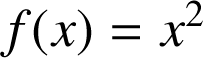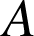est appelée l'intégrale de
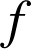sur
.
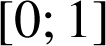On note 
. On en déduit que 
.
On en déduit qu'elles ont une limite commune.
En utilisant , on a que 
.
On a : pour tout , et 
, donc d'après le théorème des gendarmes, 
.
