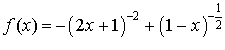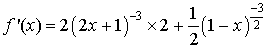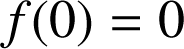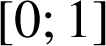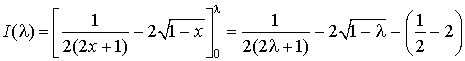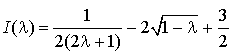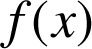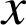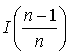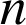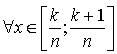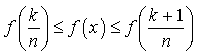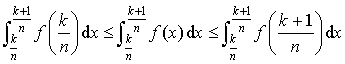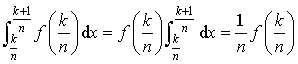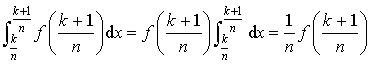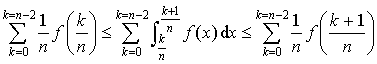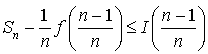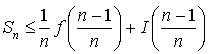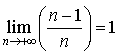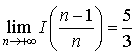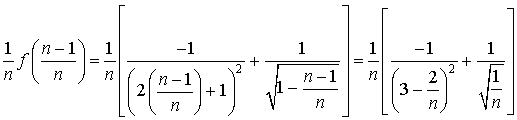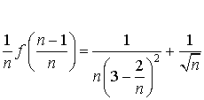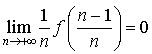Introduction
Durée : 60 minutes
Niveau : difficile
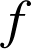 est la fonction définie sur l'intervalle
est la fonction définie sur l'intervalle
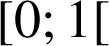 par
par 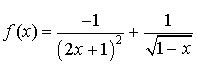 .
.
1) a. Étudier la fonction
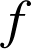 (variations / signe / limite).
(variations / signe / limite).
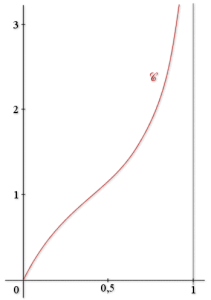
b. Tracer la courbe ![]() représentative de
représentative de
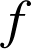 dans un repère orthogonal
dans un repère orthogonal ![]() . L'unité graphique est
. L'unité graphique est
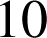 cm sur l'axe des abscisses et
cm sur l'axe des abscisses et
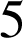 cm sur l'axe des ordonnées.
cm sur l'axe des ordonnées.
2)
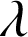 désigne un réel de l'intervalle
désigne un réel de l'intervalle
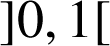 .
.
a.Calculer l'intégrale ![]() . Interpréter géométriquement cette intégrale.
. Interpréter géométriquement cette intégrale.
b. Déterminer ![]() .
.
On admettra que ![]() est l'aire en unités d'aire de la partie du plan délimitée par
est l'aire en unités d'aire de la partie du plan délimitée par ![]() , les axes de coordonnées et la droite d'équation
, les axes de coordonnées et la droite d'équation
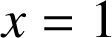 .
.
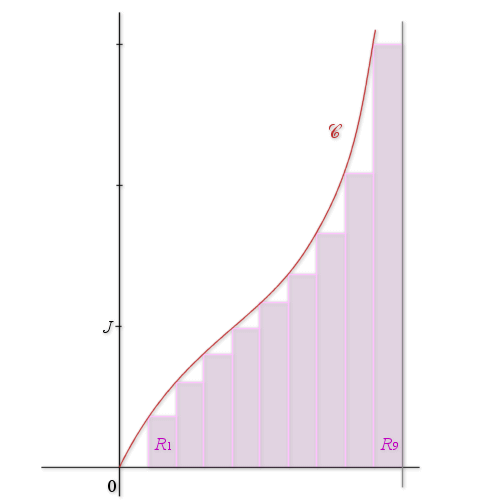
3) Le but de cette question est de calculer l'aire précédemment définie par une autre méthode (la méthode des rectangles).
Pour tout entier naturel ![]() , on pose
, on pose 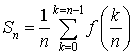 .
.
a.Interpréter graphiquement
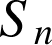 , en introduisant les rectangles
, en introduisant les rectangles
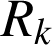 de base
de base 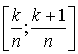 et de hauteur
et de hauteur  , où
, où ![]() . Faire la figure lorsque
. Faire la figure lorsque
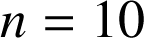 .
.
b. Prouver que pour tout entier
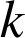 tel que
tel que ![]() ,
, 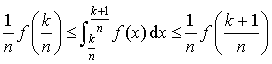 .
.
c. En déduire :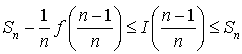 puis que :
puis que : 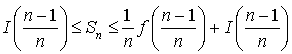 .
.
d. Déterminer enfin ![]() .
.