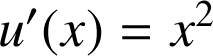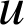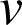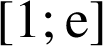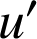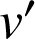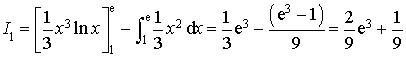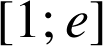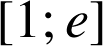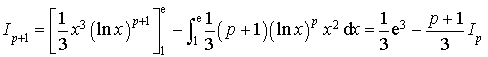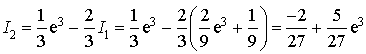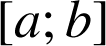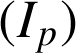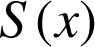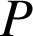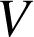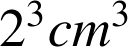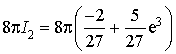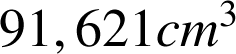Introduction
Durée : 40 minutes
Niveau : moyen
Soit
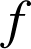la fonction définie sur
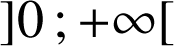par 
.
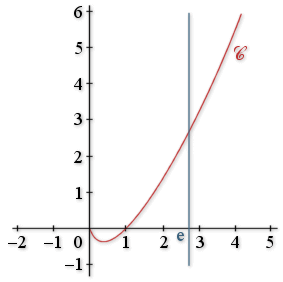
est la représentation graphique de
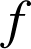dans un repère orthonormal 
du plan (unité graphique :
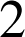cm).
On pose pour 
, 
.
1) A l'aide d'une intégration par parties, calculer 
.
2) Prouver, en effectuant une intégration par parties, que pour tout entier
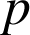supérieur ou égal à
: 
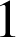3) En déduire successivement
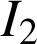et
.
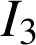4) On considère la suite 
.
Montrer que cette suite est décroissante et minorée. Que peut-on en déduire ?
5) On fait tourner autour de l'axe des abscisses l'arc de courbe constitué des points de , d'abscisses comprises entre
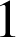et
. Le point
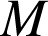de , d'abscisse
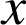, décrit alors un cercle de rayon
.
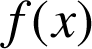Calculer le volume du solide ainsi engendré, en
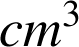. En donner une valeur approchée à
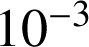près.
