Introduction
Durée : 60 minutes
Niveau : difficile
Soit
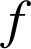 la fonction définie sur
la fonction définie sur
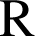 par
par ![]() .
.
On appelle ![]() la représentation graphique de
la représentation graphique de
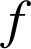 dans un repère orthonormal
dans un repère orthonormal ![]() du plan.
du plan.
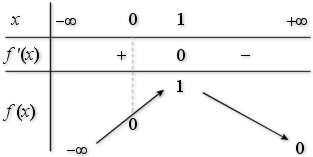
1) Etudier les variations de
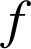 , ainsi que les limites.
, ainsi que les limites.
Dresser le tableau des variations de
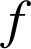 .
.
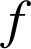 est dérivable sur
est dérivable sur
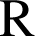 .
.
Pour tout réel
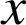 ,
, ![]() .
.
La fonction exponentielle étant strictement positive sur
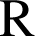 , est du signe de
, est du signe de
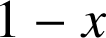 .
.
![]() ;
; ![]() ;
; ![]() .
.
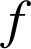 est donc strictement croissante sur
est donc strictement croissante sur
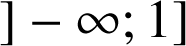 et strictement décroissante sur
et strictement décroissante sur
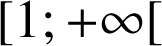 .
.
![]() et
et ![]() donc
donc ![]() .
.
Par produit, ![]() .
.
![]() ,
, ![]() .
.
![]() donc
donc ![]() .
.
Puis, ![]() .
.
2) A l'aide d'une intégration par parties, calculer ![]() .
.
![]()
Posons :
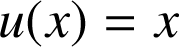 et
et
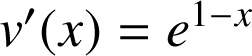 . On a alors :
. On a alors :
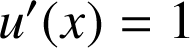 et
et
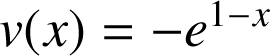 .
.
 et
et
 sont dérivables sur
sont dérivables sur
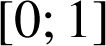 et leurs dérivées
et leurs dérivées
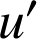 et
et
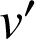 sont continues sur
sont continues sur
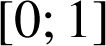 . D'après la formule d'intégration par parties, on a :
. D'après la formule d'intégration par parties, on a :
3) Soit
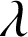 un réel positif ; on considère
un réel positif ; on considère
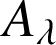 l'aire, en unités d'aire, de la partie du plan comprise entre l'axe des abscisses, la courbe, et les droites d'équation
l'aire, en unités d'aire, de la partie du plan comprise entre l'axe des abscisses, la courbe, et les droites d'équation
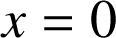 et
et
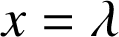 .
.
A l'aide d'une intégration par parties, calculer
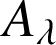 puis
puis ![]() .
.
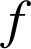 étant continue et positive sur l'intervalle
étant continue et positive sur l'intervalle ![]() ,
, ![]() .
.
En procédant comme dans la question 2) :
On retrouve la valeur de
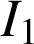 avec
avec
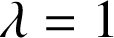 .
.
![]() et
et ![]() donc
donc ![]() .
.
Pour tout entier ![]() , on pose
, on pose ![]() .
.
1) a. Démontrer que pour tout
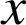 de l'intervalle
de l'intervalle
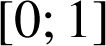 :
: ![]() .
.
b. En déduire, pour tout entier ![]() , l'encadrement :
, l'encadrement : ![]() .
.
a. Utiliser un encadrement de
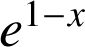 pour
pour ![]() .
.
b. Voir le cours sur la comparaison d'intégrales.
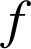 et
et
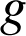 étant deux fonctions continues sur un intervalle
étant deux fonctions continues sur un intervalle
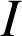 ,
,
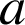 et
et
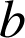 réels de
réels de
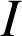 tels que
tels que ![]() , si
, si ![]() pour tout
pour tout
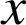 de
de
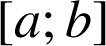 , alors :
, alors : ![]() .
.
a. Pour tout entier
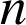 non nul et pour tout
non nul et pour tout
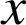 de l'intervalle
de l'intervalle
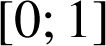 , on a :
, on a : ![]() ; comme la fonction exponentielle est croissante sur
; comme la fonction exponentielle est croissante sur
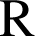 , on obtient l'encadrement :
, on obtient l'encadrement : ![]() . En multipliant par
. En multipliant par ![]() , on a :
, on a : ![]() .
.
b. En intégrant sur l'intervalle
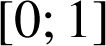 les inégalités précédentes, on a :
les inégalités précédentes, on a :
![]() ,
, ![]()
Puis, ![]() . D'où,
. D'où, ![]() .
.
2) En intégrant par parties, montrer que, pour tout ![]() :
: ![]() .
.
Faire une intégration par parties sur ![]() .
.
![]() ,
, ![]() .
.
Posons :
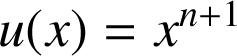 et
et
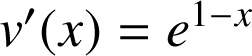 . On a alors :
. On a alors :
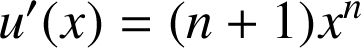 et
et
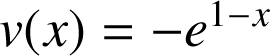 .
.
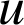 et
et
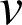 sont dérivables sur
sont dérivables sur
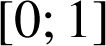 et leurs dérivées
et leurs dérivées
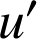 et
et
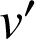 sont continues sur
sont continues sur
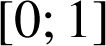 . D'après la formule d'intégration par parties, on a :
. D'après la formule d'intégration par parties, on a :
3) Pour tout entier ![]() , on pose
, on pose ![]() .
.
a. Exprimer
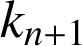 à l'aide de
à l'aide de
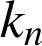 .
.
b. En raisonnant par récurrence sur
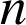 , démontrer que
, démontrer que
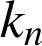 est un nombre entier pour tout entier
est un nombre entier pour tout entier ![]() .
.
c. Démontrer que pour tout entier ![]() ,
, ![]() n'est pas un nombre entier.
n'est pas un nombre entier.
d. En déduire que
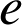 n'est pas un nombre rationnel.
n'est pas un nombre rationnel.
a. On montre que : ![]() ,
, ![]() .
.
c. Utiliser les résultats des questions (B)1.b et (B)3.b pour prouver que ![]() est strictement compris entre deux entiers consécutifs.
est strictement compris entre deux entiers consécutifs.
d. Penser à utiliser un raisonnement par l'absurde.
d. On peut raisonner par l'absurde et supposer ![]() ,
,
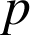 et
et
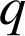 entiers non nuls.
entiers non nuls.
a. ![]() ,
,
b. Soit
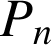 la proposition : «
la proposition : «
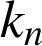 est un entier ».
est un entier ».
Au rang initial
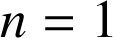 ,
, ![]() est vérifiée.
est vérifiée.
Supposons
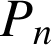 vraie pour un entier
vraie pour un entier ![]() ; d'après l'expression de
; d'après l'expression de
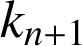 , si
, si
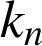 est un entier alors
est un entier alors
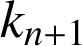 est un entier.
est un entier.
D'après le principe de récurrence,
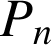 est vraie pour tout entier
est vraie pour tout entier ![]() .
.
c. D'après 1.b), ![]() donc
donc ![]() . Or,
. Or,
![]() ,
, 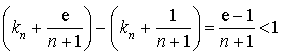 , donc, puisque
, donc, puisque
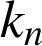 est un entier,
est un entier, ![]() est strictement compris entre deux entiers consécutifs. Ainsi,
est strictement compris entre deux entiers consécutifs. Ainsi, ![]() n'est pas un entier.
n'est pas un entier.
d. On raisonne par l'absurde. Supposons que
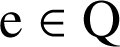 , autrement dit
, autrement dit ![]() ,
,
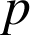 et
et
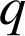 entiers non nuls.
entiers non nuls.
![]() ,
, 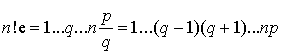 . Donc
. Donc ![]() est un entier, ce qui est en contradiction avec le résultat de la question précédente.
est un entier, ce qui est en contradiction avec le résultat de la question précédente.
Conclusion :
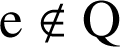 .
.






