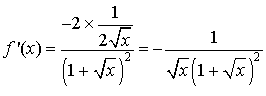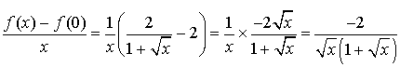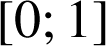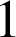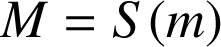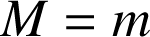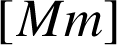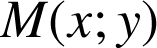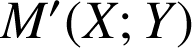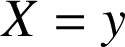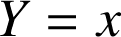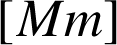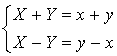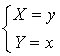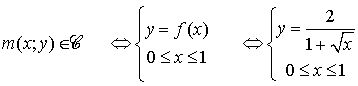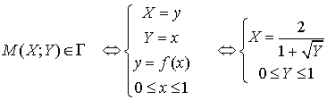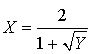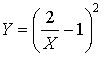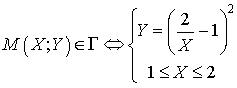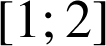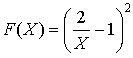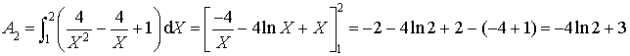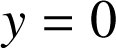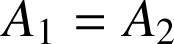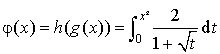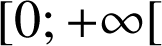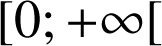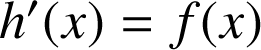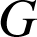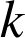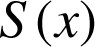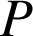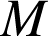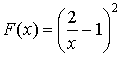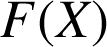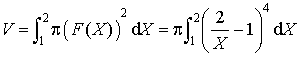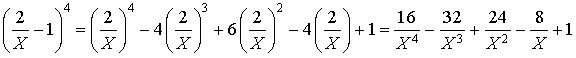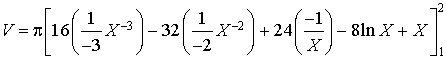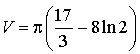Introduction
Durée : 90 minutes
Niveau : difficile
Soit
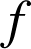 la fonction définie sur
la fonction définie sur
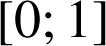 par :
par : 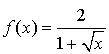 .
.
On appelle ![]() sa courbe représentative dans un repère orthonormal
sa courbe représentative dans un repère orthonormal ![]() du plan (unité graphique :
du plan (unité graphique :
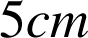 ).
).
Le but de l'exercice est de calculer de deux façons l'intégrale ![]() .
.
1) a. Calculer
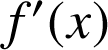 pour tout
pour tout
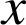 de
de
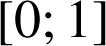 .
.
Etudier la dérivabilité de
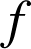 en
en
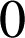 . Que peut-on en déduire pour la courbe
. Que peut-on en déduire pour la courbe ![]() ?
?
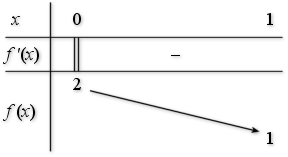
b. Donner le tableau de variation de
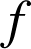 et construire la courbe
et construire la courbe ![]() .
.
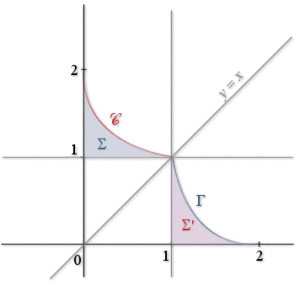
c. On note
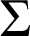 la partie du plan, limitée par la courbe
la partie du plan, limitée par la courbe ![]() , les droites d'équations
, les droites d'équations
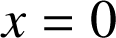 ,
,
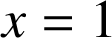 et la droite d'équation
et la droite d'équation
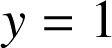 .
.
Hachurer la surface
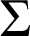 .
.
On note
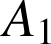 l'aire de
l'aire de
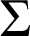 exprimée en unités d'aire. Exprimer
exprimée en unités d'aire. Exprimer
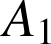 à l'aide d'une intégrale.
à l'aide d'une intégrale.
2) Une première méthode de calcul de l'intégrale I.
Soit
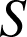 la réflexion d'axe
la réflexion d'axe
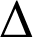 d'équation
d'équation
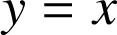 .
.
a. Soit
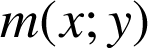 un point du plan et
un point du plan et
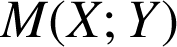 l'image par
l'image par
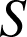 du point
du point
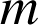 .
.
Exprimer
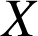 et
et
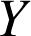 en fonction de
en fonction de
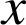 et
et
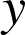 .
.
b. Soit ![]() l'image de la courbe
l'image de la courbe ![]() par la réflexion
par la réflexion
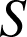 . Donner une relation liant
. Donner une relation liant
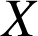 et
et
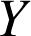 dans le cas où
dans le cas où
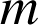 appartient à
appartient à ![]() . En déduire une équation cartésienne de la courbe
. En déduire une équation cartésienne de la courbe ![]() de la forme
de la forme
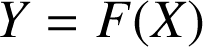 .
.
Quel est l'ensemble de définition de la fonction
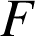 ?
?
c. Construire la courbe ![]() sur le même graphique que
sur le même graphique que ![]() .
.
d. Soit
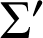 la partie du plan limitée par la courbe
la partie du plan limitée par la courbe ![]() , l'axe des abscisses et la droite
, l'axe des abscisses et la droite
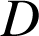 d'équation
d'équation
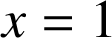 .
.
On note
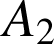 l'aire de
l'aire de
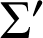 exprimée en unités d'aire.
exprimée en unités d'aire.
Exprimer
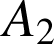 à l'aide d'une intégrale, puis calculer
à l'aide d'une intégrale, puis calculer
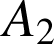 .
.
En déduire la valeur de ![]() .
.
3) Méthode de calcul avec changement de variable.
On appelle
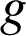 et
et
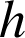 les fonctions définies sur
les fonctions définies sur
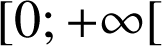 par :
par :
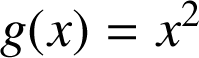 et
et 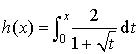 .
.
On note
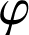 la fonction
la fonction ![]() définie sur
définie sur
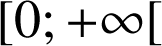 .
.
a. Exprimer
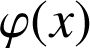 à l'aide d'une intégrale. Calculer
à l'aide d'une intégrale. Calculer
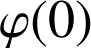 .
.
b. Après avoir justifié la dérivabilité de
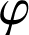 sur
sur
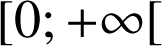 , exprimer
, exprimer
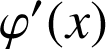 à l'aide des fonctions
à l'aide des fonctions
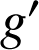 et
et
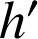 . Calculer
. Calculer
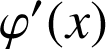 pour
pour
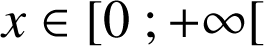 .
.
c. Déterminer deux réels
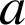 et
et
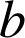 tels que, pour tout
tels que, pour tout ![]() :
: ![]() .
.
En déduire les primitives de la fonction ![]() sur
sur
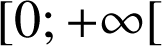 .
.
d. Donner l'expression de
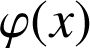 pour
pour
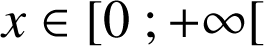 .
.
En déduire la valeur de
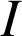 .
.
4) Soit
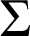 la partie du plan définie à la question 1.c) ; on considère alors le solide de révolution engendré par la rotation de
la partie du plan définie à la question 1.c) ; on considère alors le solide de révolution engendré par la rotation de
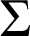 autour de l'axe
autour de l'axe ![]() .
.
a. Donner une formule permettant de calculer le volume de ce solide à l'aide d'une intégrale.
b. Calculer
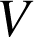 , exprimé en unités de volume.
, exprimé en unités de volume.