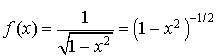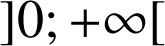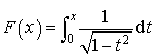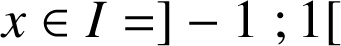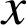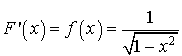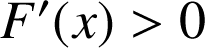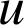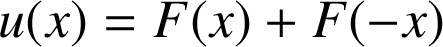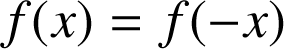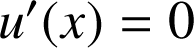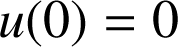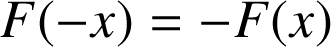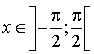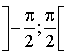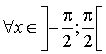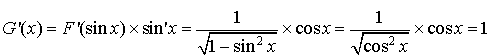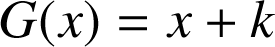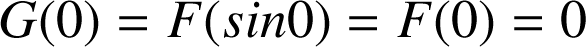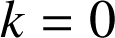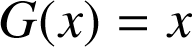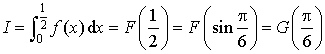Introduction
Durée : 30 minutes
Niveau : moyen
On considère la fonction
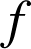définie sur l'intervalle
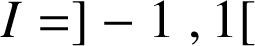par 
.
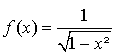1) Justifier l'existence et l'unicité d'une primitive
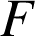de
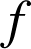sur
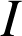s'annulant en
.
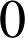Exprimer
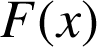à l'aide d'une intégrale.
2) Etudier le sens de variation de
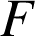sur
.
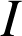4) Soit
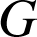la fonction définie sur
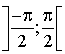par 
.
a. Montrer que
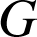est dérivable sur 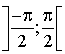et calculer
.
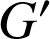b. En déduire une expression simple de
.
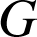5) Calculer l'intégrale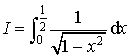 
.
