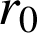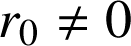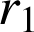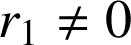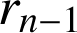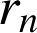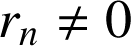Méthode
A l'aide de la décomposition en nombres premiers
Soit
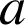 et
et
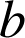 deux entiers naturels non nuls.
deux entiers naturels non nuls.
![]() et
et ![]() .
.
![]() sont des nombres premiers distincts.
sont des nombres premiers distincts.
![]() et
et ![]() sont des entiers naturels éventuellement nuls.
sont des entiers naturels éventuellement nuls.
![]()
![]() pour tout indice
pour tout indice
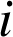 vérifiant :
vérifiant : ![]() .
.
Exemple
Déterminer ![]() .
.
![]() et
et ![]() donc
donc ![]() .
.
Définition
A l'aide de l'algorithme d'Euclide
Soit
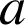 et
et
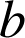 sont deux entiers naturels non nuls.
sont deux entiers naturels non nuls.
La suite des divisions euclidiennes :
de
|
| avec |
de
|
| avec |
de
|
| avec |
de
|
| avec |
permet de définir une suite
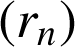 strictement décroissante d'entiers positifs.
strictement décroissante d'entiers positifs.
Le dernier reste non nul est alors le
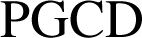 de
de
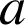 et
et
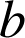 (si
(si
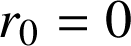 , alors c'est
, alors c'est
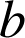 ).
).
Exemple
Déterminer le ![]()
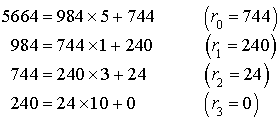
Donc ![]() .
.