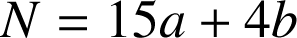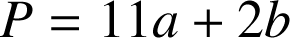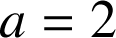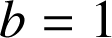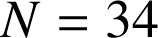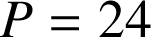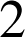Soit
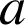et
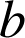deux entiers naturels non nuls.
On pose 
et 
.
1) Montrer que tout diviseur
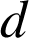commun de
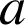et
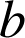est un diviseur commun de
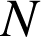et
.
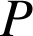2) La réciproque est-elle vraie ? C'est-à-dire tout diviseur
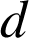commun de
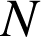et
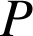est-il un diviseur de
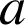et
?
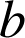