Une équation diophantienne est une équation à coefficients entiers, et dont les inconnues sont entières.
On résout ces équations dans l'ensemble des couples d'entiers relatifs ![]() .
.
On pose : ![]() ;
;
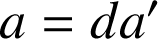 ,
,
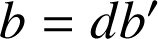 avec
avec
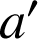 et
et
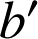 premiers entre eux.
premiers entre eux.
![]() avec
avec
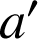 et
et
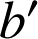 premiers entre eux.
premiers entre eux.
D'après le théorème de Bezout, il existe deux entiers relatifs
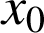 et
et
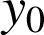 tels que :
tels que : ![]() .
.
Soit
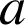 et
et
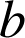 deux entiers naturels non nuls ;
deux entiers naturels non nuls ;
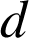 est leur
est leur
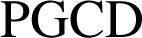 .
.
D'après le théorème de Bezout il existe deux entiers relatifs
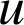 et
et
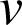 tels que :
tels que :
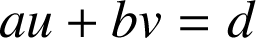 .
.
Le but est de donner un algorithme permettant de déterminer
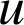 et
et
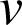 .
.
On met en œuvre l'algorithme d'Euclide et on calcule les restes successifs en fonction de
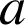 et
et
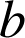 .Le dernier reste non nul est le
.Le dernier reste non nul est le
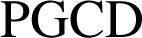 . On développe alors les calculs de façon à faire apparaître à chaque étape une écriture du reste de la forme
. On développe alors les calculs de façon à faire apparaître à chaque étape une écriture du reste de la forme
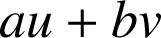 .
.
Déterminons des entiers relatifs
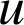 et
et
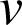 tels que :
tels que :
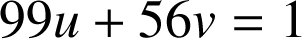 .
.
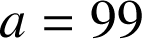 et
et
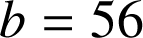 .
.
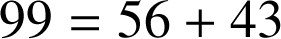 soit
soit
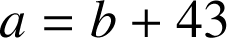 donc
donc
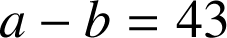 ,
,
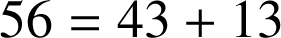 soit
soit
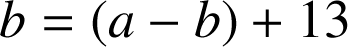 donc
donc
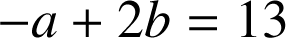 ,
,
 soit
soit
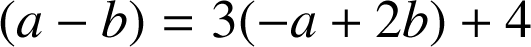 donc
donc
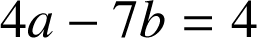 ,
,
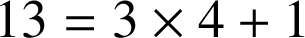 soit
soit
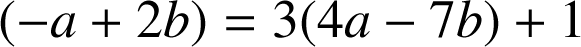 donc
donc
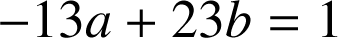 ,
,
 .
.
Par conséquent, on a :
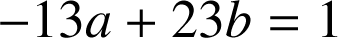 ;
;
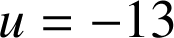 et
et
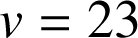 .
.
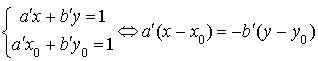
Or 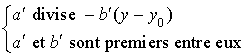
D'après le théorème de Gauss,
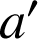 divise
divise ![]() , ce qui équivaut à : « il existe un entier relatif
, ce qui équivaut à : « il existe un entier relatif
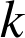 tel que
tel que ![]() ».
».
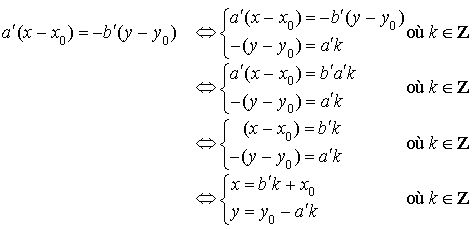
Les solutions sont les couples de la forme ![]() avec
avec
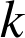 dans
dans
 .
.






