5.3.2.2 - Neighbor-joining (Saitou et Nei 1987)
La méthode du Neighbor-joining[1] est basée sur le principe d'évolution minimale qui fait l'hypothèse que l'arbre vrai est l'arbre de plus petite longueur tel que les longueurs de ses branches décrivent le plus fidèlement possible les distances évolutives entre les taxons considérés.
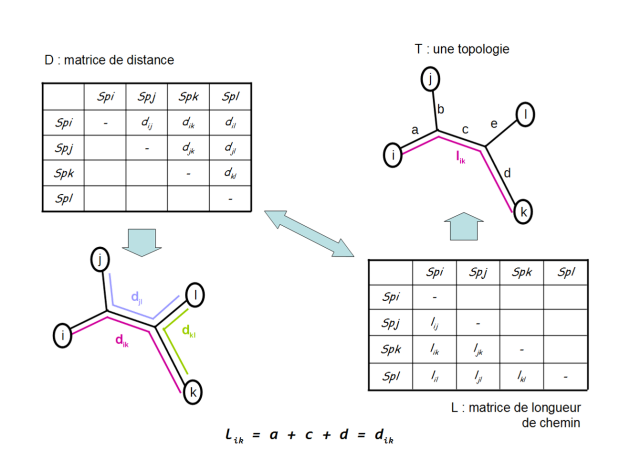
Attention : Notion d'arbre additif
Dans un arbre additif, chaque branche de l'arbre peut être décrite par une valeur qui représenta sa longueur. Lorsque l'arbre est additif, la longueur d'un trajet entre deux feuilles sur l'arbre est égale à la somme des longueurs des branches qui sont traversées pour passer d'une feuille à l'autre (fig. 5.45).
Sur la base d'une matrice de distances évolutives estimées entre tous les couples d'OTU, l'algorithme du neighbor-joining [1] permet de produire un arbre additif de longueur minimale[2] :
qui représente le mieux les distances évolutives estimées à partir des données,
pour lequel les branches séparant deux OTU de leur ancêtre commun peuvent être de longueurs différentes.
C'est une méthode qui tolère dans une certaine mesure des écarts au principe de l'horloge moléculaire.
Méthode :
A partir d'un arbre initial en étoile constitué d'un unique ancêtre commun à toutes les feuilles, la méthode du neighbor-joining vise à isoler récursivement les couples d'OTU (ou groupes d'OTU) qui partagent un ancêtre commun de telle sorte que l'arbre soit de longueur minimale.
A partir d'un arbre en étoile constitué d'un unique nœud ancestral :
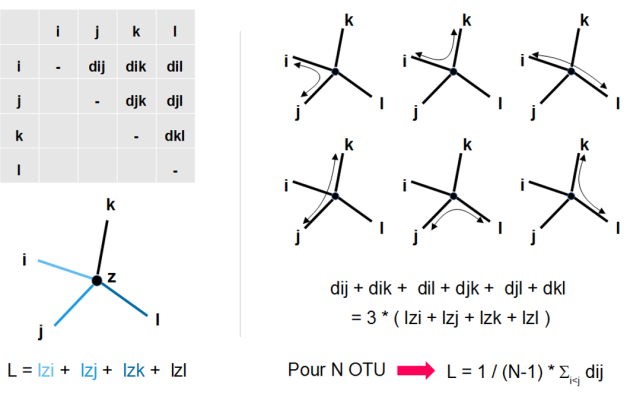
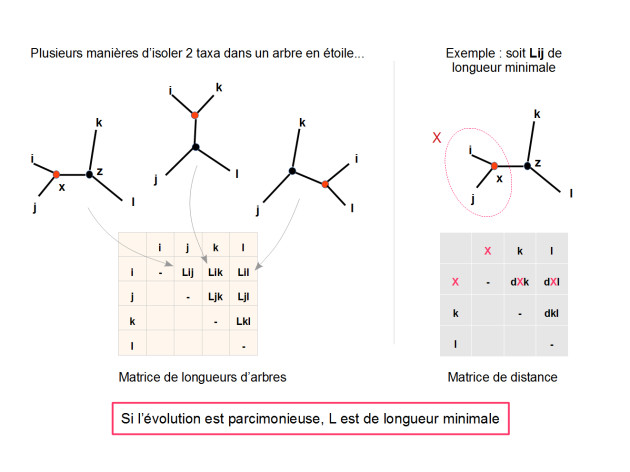
Sur la base des distances évolutives dans la matrice, calculer la longueur de l'arbre (fig. 5.46)
extraire un couple d'OTU (i,j) et faire l'hypothèse qu'ils partagent un ancêtre commun (X)
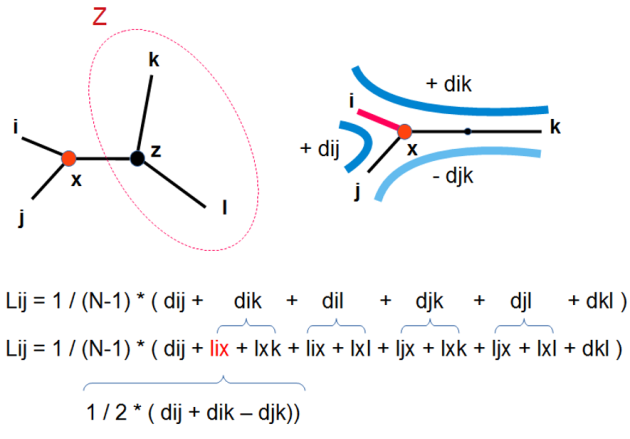
Recalculer les longueurs des branches de l'arbre incluant l'ancêtre du couple (i,j) : LiX, LjX, LXZ (ou Z représente le reste de l'arbre) (fig. 5.47)
Calculer la longueur de l'arbre L(i,j) et stocker cette valeur dans une matrice de longueur d'arbre
Répéter ces opérations pour l'ensemble des coupes d'OTU possibles et compléter la matrice des longueur d'arbres en conséquence
Identifier le couple d'OTU qui produit un arbre de longueur minimale (la plus petite valeur dans la matrice de longueurs d'arbres), et retenir l'arbre correspondant. Il constituera le nouvel arbre partiellement résolu (fig. 5.48).
Recalculer la matrice de distance entre OTU en remplaçant les OTU i et j par leur groupe monophylétique (i, j)
Répéter l'ensemble des opérations précédentes jusqu'à ce que l'ensemble des relations de filiation soient résolues (chaque ancêtre à au plus deux descendants)
Interprétation
Avec la méthode de Neighbor-Joining, l'arbre est de longueur minimale[3]. Les longueurs de branche sont la représentation du nombre de substitutions qui se sont produites au cours du temps. La recherche d'un arbre de longueur minimale sous entend que l'on considère ici que l'évolution implique un minimum d'événements évolutifs (un minimum de substitutions). Les longueurs des branches reflètent également le temps qui s'écoule sous condition que la molécule analysée respecte le principe de l'horloge moléculaire. Lorsque l'horloge moléculaire n'est pas respectée, les longueurs des branches depuis un ancêtre commun seront de longueurs différentes, traduisant une vitesse différente dans l'accumulation des substitutions entre deux lignées au cours d'un même intervalle de temps.
Par construction, c'est l'ensemble de l'arbre qui est évalué indépendamment de la proximité évolutive des OTU considérés. Il n'est donc pas orienté dans le temps. L'arbre n'est pas raciné.
Attention : Comparaison des méthodes UPGMA et neighbor-joining
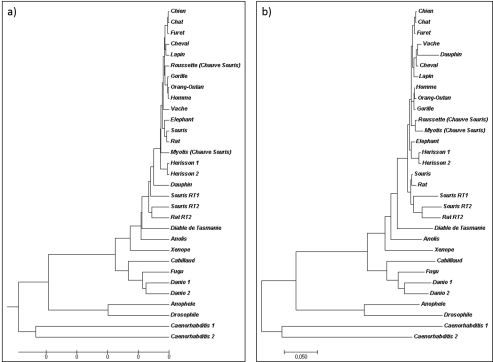
Nous vous rappelons que la méthode UPGMA contrairement au neighbor-joining n'est pas en mesure de tenir compte des variations de vitesses évolutives. Ainsi dans un arbre comme ceux présentés figure 5.49, l'axe horizontal représentera :
le temps absolu avec une précision discutable dans un arbre UPGMA
une combinaison du temps et de la vitesse évolutive différentielle entre OTU dans un arbre NJ
Cela se traduira viuellement par un alignement des OTU au point t0 dans l'arbre UPGMA (fig5.49a)et, dans l'arbre NJ, par un déport plus ou moins prononcé vers la droite de ces mêmes OTU en fonction de leur vitesse évolutive (fig5.49b).