5.3.1 - L'approche cladistique : analyse au maximum de parcimonie
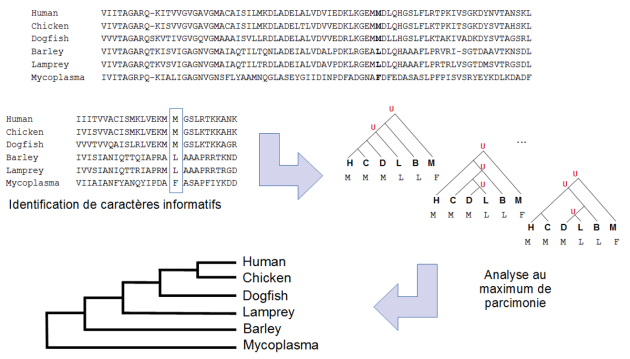
On fait ici l'hypothèse que la vraie histoire évolutive est celle qui implique le moins d'événements évolutifs (fig. 5.38).
L'algorithme de Fitch[1] permet, pour une topologie et un caractère informatif donné, d'inférer les états ancestraux du caractère qui minimise le nombre d'événements évolutifs dans l'ensemble de l'arbre. A partir d'une topologie racinée arbitrairement elle permet, par le parcours de la topologie depuis les feuilles jusqu'à la racine, d'inférer l'ensemble des états possibles du caractère considéré pour chacun des ancêtres analysés, et de déterminer le nombre minimal d'événements évolutifs nécessaires pour expliquer la répartition des états du caractère aux feuilles. Généralisé à l'ensemble des caractères considérés et à l'ensemble des topologies possibles, l'application de cet algorithme permet de résoudre la phylogénie au maximum de parcimonie[2]. Il est à noter toutefois que lorsque le nombre d'OTU est grand, cette méthode exacte de résolution est trop lente et des heuristiques[3] sont mises en œuvre.
Méthode : Maximum de parcimonie
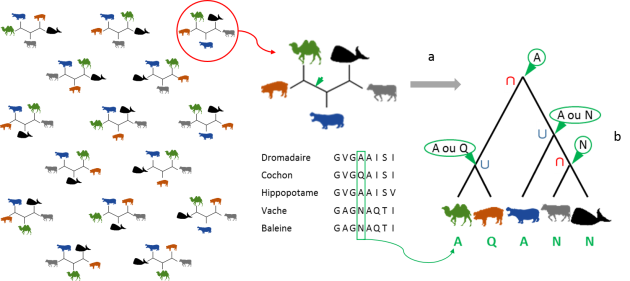
L'algorithme de Fitch permet de rechercher l'arbre impliquant le minimum d'événement pour un caractère et une topologie (petite parcimonie) (fig. 5.39) :
Raciner la topologie de façon arbitraire
A partir des feuilles, pour chaque paire de nœud et leur ancêtre commun immédiat, appliquer les règles suivantes :
Si les fils du nœud portent des états différents : faire une union (U)
→ attribuer au père l'ensemble des informations portées par les fils
Si les fils du nœud portent des états semblables : faire une intersection (∩)
→ attribuer au père uniquement les informations communes aux fils.
Appliquer ce principe récursivement depuis les feuilles jusqu'à la racine. Le nombre minimum d'événements évolutifs pour ce caractère et cette topologie est le nombre d'événements d'union réalisé sur la topologie (document C1). Généralisé à l'ensemble des caractères considérés et l'ensemble des topologies possibles, l'application de cet algorithme permet d'identifier la topologie au maximum de parcimonie (grande parcimonie). Celle-ci correspond à la topologie pour laquelle la somme de valeurs de parcimonie estimées pour chaque caractère informatif analysés sera minimale.
\(Grande\:parcimonie =MIN[ensemble\:des\:topologies]\: [\sum (caract.\: info.)\:(petite\: parcimonie)]\)