Produit de convolution et fonction de transfert
Il existe un rapport intime entre la description d'un système par le produit de convolution et sa fonction de transfert. Nous allons l'étudier à travers un exemple, le circuit RC passe-bas rencontré au chapitre 3.
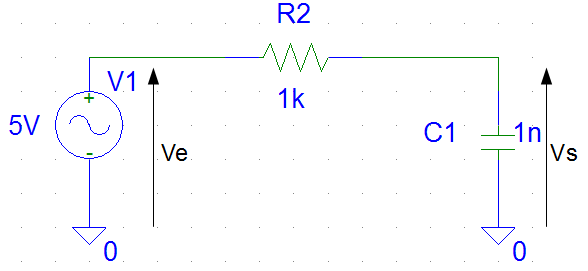
Soit le circuit RC suivant et sa fonction de transfert (cf. chapitre 3) :
L'idée de ce paragraphe est de regarder les différentes modélisations qu'on peut faire de ce système et surtout de constater qu'elles sont autant de facettes de la même réalité. Nous montrerons aussi les liens intimes qui existent entre ces modélisations.
La représentation complexe qui correspond au fonctionnement du circuit en régime permanent découle de l'équation différentielle (en tension) suivante :
La résolution de l'équation différentielle pour une entrée quelconque permet de déterminer la sortie de ce système causal, linéaire et invariant, soit
. On peut parler de modélisation structurelle dans la mesure où il est nécessaire de connaître la structure du système pour pouvoir le résoudre.
Un cas classique d'entrée correspond à la charge du condensateur à tension constante ce qui correspond à
où E est une source de tension constante et 
la fonction de heaviside, appelée aussi fonction échelon (représentez la graphiquement pour comprendre pourquoi) définie comme suit :
Cela signifie en somme que la source de tension constante E est appliquée au système à partir de t=0.
La résolution de l'équation différentielle :
est classique (cf. un cours d'électrocinétique de niveau L1) et conduit à :
avec 
constante du temps du système.
Il faut bien comprendre que le concept de fonction de transfert correspond au cas particulier du régime dit harmonique dans lequel l'entrée est une fonction trigonométrique (cosinus ou sinus à une fréquence donnée), qui plus est en régime permanent, c'est-à-dire lorsque le transitoire s'est éteint. La modélisation en fonction de transfert est également structurelle en ce sens qu'il faut connaître les impédances complexes des composants qui constituent le circuit.
Nous en venons à présent à la modélisation fonctionnelle qui ne nécessite que la connaissance de la réponse impulsionnelle du circuit. Certes, la connaissance de cette réponse impulsionnelle ne coule pas de source. On peut envisager de la déterminer expérimentalement mais l'entrée impulsion de Dirac est une abstraction impossible à réaliser expérimentalement de façon rigoureuse. Faisons néanmoins l'hypothèse que nous la connaissons. Nous admettons qu'elle s'écrit :
pour 
et 
pour 
(on se souvient que pour respecter la causalité, la réponse impulsionnelle doit être nulle pour t négatif).
Nous pouvons à présent calculer la sortie du système correspondant à l'entrée, 
par le produit de convolution :
On a pris u comme variable muette dans l'intégrale de convolution plutôt que τ en raison de la constante de temps déjà baptisée τ.
Le calcul de la sortie par la modélisation fonctionnelle (produit de convolution) coïncide bien avec la modélisation structurelle (résolution de l'équation différentielle).
Il reste à trouver dans ces différentes modélisations la place de la fonction de transfert, soit :
Nous allons sur cet exemple constater que la fonction de transfert du système n'est autre que la transformée de Fourier de sa réponse impulsionnelle et nous démontrerons plus loin que c'est un théorème valable pour tout système.
Calculons donc la transformée de Fourier de 
:
On a bien vérifié que la fonction de transfert du système est la transformée de Fourier de sa réponse impulsionnelle.
Le lien ci-dessus permet de télécharger le fichier qui contient la réponse impulsionnelle d'un espace caractéristique.
