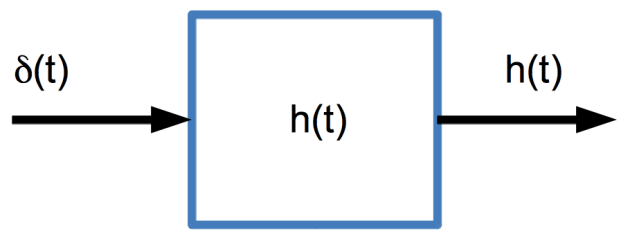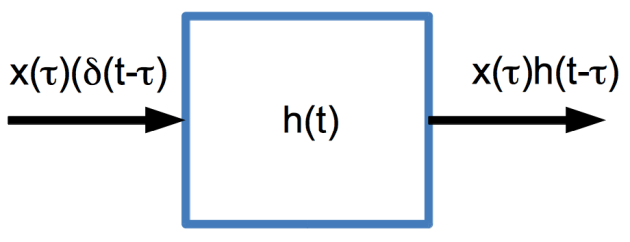Produit de convolution
Nous allons démontrer ici que la connaissance de la réponse impulsionnelle permet de déterminer la sortie pour une entrée quelconque ce qui est une conséquence des hypothèses de linéarité et d'invariance.
Remarque : il est difficile d'imaginer un système physique non causal, la causalité étant une hypothèse fondamentale en physique qui n'a jamais été prise en défaut. Par contre, invariance et linéarité ne sont pas systématiques : il faut bien comprendre que le concept de convolution repose sur ces hypothèses satisfaites.
Pour mettre en évidence le produit de convolution, il suffit de construire un signal d'entrée comme combinaison linéaire d'impulsions de Dirac selon la suite de la figure ci-dessous :
Si on met un Dirac en entrée, on obtient la réponse impulsionnelle en sortie (par définition de la réponse impulsionnelle) :
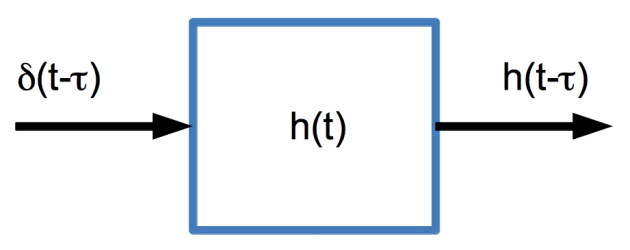
Si on décale temporellement ce Dirac, on obtient par invariance, la réponse impulsionnelle décalée d'autant :
Si on affecte à présent, un coefficient multiplicateur à ce Dirac décalé, soit 
, on obtient, par linéarité :
Il ne reste plus maintenant qu'à superposer une infinité de tels Dirac décalés et coefficientés en entrée, soit :
que nous avons déjà rencontré au chapitre 6 et que nous avions interprété comme combinaison linéaire dans la base (infinie) des impulsions de Dirac décalées lorsque t varie de moins l'infini à plus l'infini. C'est la fameuse représentation vectorielle d'un signal écrit comme combinaison linéaire de la base canonique formée par les Dirac décalés.
Par linéarité encore, le signal réagit à cette entrée par la combinaison linéaire :
qui définit le produit de convolution qu'on écrit :
Le produit de convolution est donc défini dans le contexte des systèmes causaux, linéaires et invariants. Mais on peut le généraliser : soient 
et 
deux signaux de 
, on appelle produit de convolution de ces deux signaux et on note :
Comme pour l'intégrale de Fourier, on ne représente pas explicitement les bornes d'intégration qui sont a priori moins l'infini et plus l'infini.
Nous admettons les propriétés de commutativité, associativité et distributivité par rapport à l'addition du produit de convolution pour les fonctions de 
.
