Valeur moyenne
On peut dans le contexte du signal représenté par un vecteur dans 
définir aisément le concept de valeur moyenne du signal par la formule triviale familière à n'importe quel étudiant habitué à calculer sa moyenne dans un module dans lequel il a obtenu N notes.
Si la valeur moyenne d'un signal n'a pas de signification physique immédiate, elle permet de faire une première transition vers la représentation vectorielle du signal analogique de façon intuitive mais néanmoins rigoureuse.
En se souvenant que la durée totale du signal s'écrit 
, on peut réécrire l'équation précédente :
A présent, si on diminue Te, on densifie l'échantillonnage et à la limite, si on pose Te=dt qui tend vers 0, le signal échantillonné tend vers le signal analogique, la somme tend vers une somme qui comporte un nombre infini de termes et la formule précédente devient :
Par passage à la limite dt tend vers 0, l'échantillon xi tend vers la valeur instantanée x(t) et l'intégrale porte sur la durée T totale du signal.
Exemple :
On peut interpréter la moyenne 
comme étant l'approximation de l'intégrale
par la méthode des rectangles comme l'illustre la figure ci-dessous :
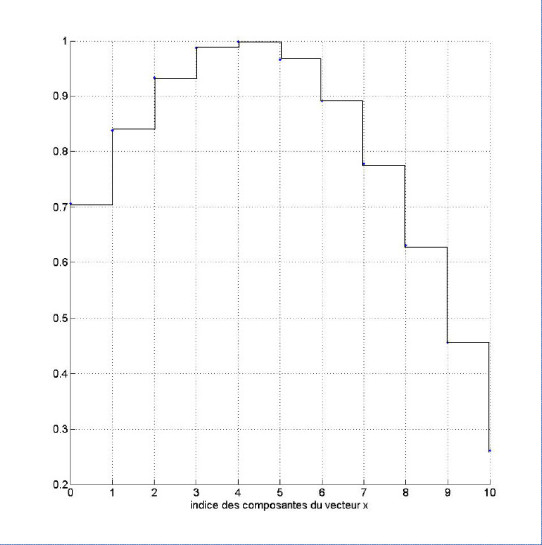
signal/vecteur scilab et intégration par la méthode des rectangles. L'approximation est d'autant meilleure que l'échantillonnage est fin.
Il importe de comprendre qu'on obtient le signal analogique à partir du signal échantillonné avec une densification de l'échantillonnage ce qui correspond à augmenter la dimension de l'espace vectoriel du signal jusqu'à l'infini, à durée totale du signal constante. Il faut ainsi voir dans la fonction x(t), un vecteur d'un espace vectoriel de dimension infinie. Bien que le passage de la dimension N finie à la dimension infinie soit mathématiquement délicate, elle est néanmoins rigoureuse et féconde. Nous nous contenterons ici d'admettre que les mathématiques offrent un cadre formel cohérent et rigoureux et nous nous satisferons des justifications intuitives.
