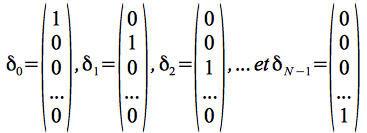Premier contact
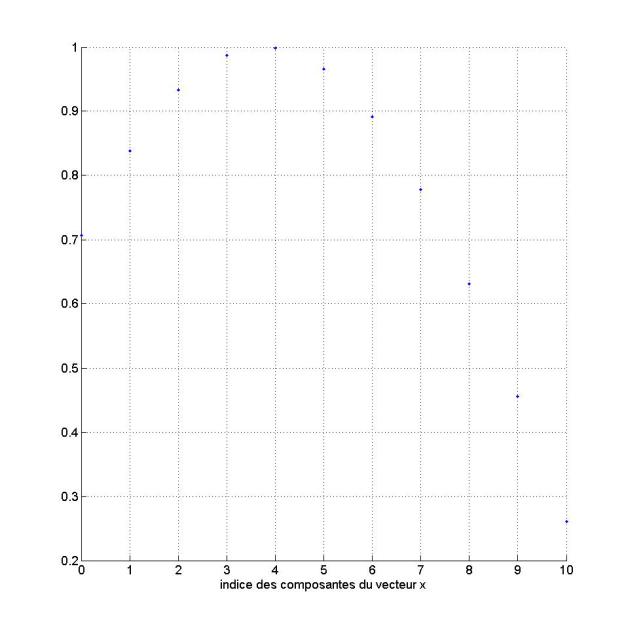
Exemple :
Sous cette forme, on voit que le signal échantillonné peut être interprété comme étant un vecteur dans un espace vectoriel de dimension N. L'équation précédente est alors lue comme la représentation du vecteur du signal dans la base canonique des vecteurs![]() qui forme un ensemble de vecteurs orthonormés, une base de l'espace des signaux de
qui forme un ensemble de vecteurs orthonormés, une base de l'espace des signaux de ![]() . Autrement dit, le signal échantillonné n'est guère différent de nos bons vieux vecteurs
. Autrement dit, le signal échantillonné n'est guère différent de nos bons vieux vecteurs![]() et
et ![]() , objets familiers s'il en est, à ceci près qu'on passe d'un espace vectoriel de dimension généralement 3 en géométrie euclidienne parce qu'attaché à notre univers physique, ici à un espace de dimension N où N est le nombre d'échantillons prélevés sur le signal. Au prix de cette abstraction près, on se retrouve ainsi dans un espace conceptuel familier dans lequel les notions classiques, distances, normes, produits scalaires, se généralisent aisément et prennent du sens. Nous allons commencer par définir des grandeurs assez intuitives, étudier le passage du signal échantillonné vers le signal analogique, puis ensuite généraliser aux grandeurs géométriques classiques en insistant sur leurs significations dans le contexte du signal.
, objets familiers s'il en est, à ceci près qu'on passe d'un espace vectoriel de dimension généralement 3 en géométrie euclidienne parce qu'attaché à notre univers physique, ici à un espace de dimension N où N est le nombre d'échantillons prélevés sur le signal. Au prix de cette abstraction près, on se retrouve ainsi dans un espace conceptuel familier dans lequel les notions classiques, distances, normes, produits scalaires, se généralisent aisément et prennent du sens. Nous allons commencer par définir des grandeurs assez intuitives, étudier le passage du signal échantillonné vers le signal analogique, puis ensuite généraliser aux grandeurs géométriques classiques en insistant sur leurs significations dans le contexte du signal.