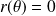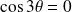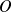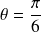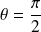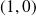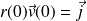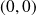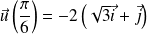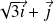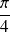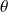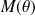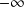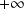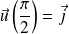Exo 12
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère le plan affine euclidien
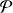de repère orthonormé
.
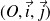Question
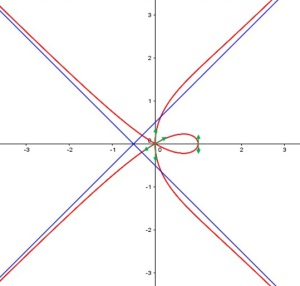
Construire la courbe
de représentation polaire :
.
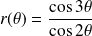La fonction
est définie sur
.
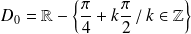Réduction de l'étude
La fonction
est périodique de période
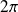.Donc on réduit l'étude à
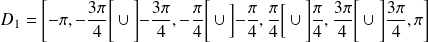.On obtient ainsi toute la courbe.
La fonction
est paire :
et
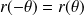.Donc on réduit l'étude à
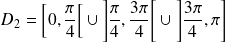.On complètera la courbe par symétrie par rapport à la droite
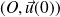, donc par rapport à l'axe des abscisses.De plus :
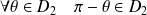et
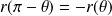.Donc on réduit l'étude à
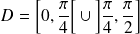.On complètera la courbe par symétrie par rapport à la droite
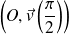, donc aussi par rapport à l'axe des abscisses.
En fait :
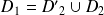avec
.
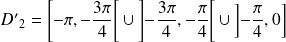Or :
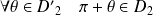et
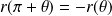, donc :
.
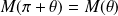Donc les arcs de courbe correspondan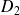t à
et à
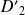sont confondus.
Etude asymptotique
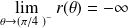et
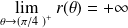. Donc on étudie la limite de
.
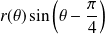Or :
.
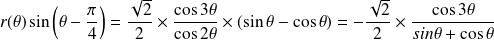Donc :
.
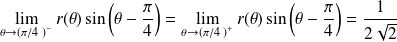Donc la courbe admet une asymptote oblique d'équation
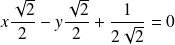, donc d'équation
.
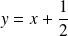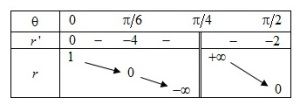
Etude des variations
La fonction
est de classe
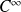sur
.
.
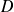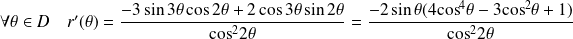Or le polynôme
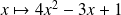a un discriminant négatif.
Donc :
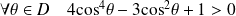, et donc :
.
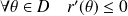De plus sur
,
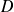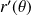ne s'annule que pour
.
Tableau de variations
Donc la courbe passe par le pôle
|  |
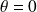Courbe
On complète ensuite la courbe par symétrie par rapport à l'axe des abscisses. |  |
