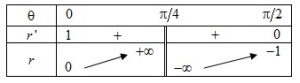
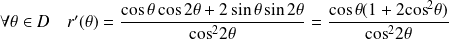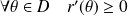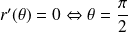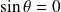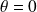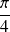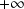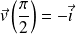Etude d'une courbe plane en coordonnées polaires
On suppose que le plan affine euclidien
 est rapporté à un repère orthonormal
est rapporté à un repère orthonormal
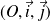 .
.
Rappel : Il existe une bijection entre le plan
 et le corps des complexes. A tout point
et le corps des complexes. A tout point
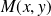 du plan, on peut associer son affixe
du plan, on peut associer son affixe
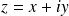 .
.
Définition :
Une courbe plane en coordonnées polaires est définie par la donnée d'un intervalle
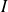 et d'une fonction
et d'une fonction
 de classe
de classe
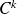 de
de
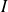 dans
dans
 avec
avec
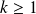 .
.
Pour tout
 , le point
, le point
 de
de
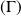 est le point d'affixe
est le point d'affixe
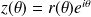 .
.
Il s'agit d'un cas particulier de paramétrage. Les points de
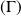 sont définis par :
sont définis par :
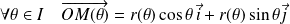 .
.
Exemple :
 est la courbe de représentation polaire
est la courbe de représentation polaire
 .
.
La fonction
 est définie sur
est définie sur
 .
.
Attention :
Attention ! La fonction
 n'est pas nécessairement positive, donc
n'est pas nécessairement positive, donc
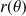 n'est pas toujours égal au module de
n'est pas toujours égal au module de
 .
.
Donc il n'y a pas unicité de la représentation polaire : si l'on change
 en
en
 et
et
 en
en
 , on obtient le même point.
, on obtient le même point.
C'est le cas de l'exemple précédent :
 . Donc les points
. Donc les points
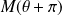 et
et
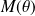 sont confondus.
sont confondus.
Fondamental :
Dans toute la suite, on note
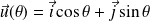 et
et
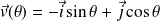 .
.
Donc :
 .
.
La vitesse est :
 .
.
L'accélération est :
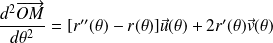 .
.
Le vecteur
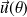 est colinéaire à
est colinéaire à
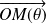 et le vecteur
et le vecteur
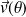 est orthogonal à
est orthogonal à
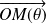 .
.
De plus, le vecteur
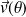 est le vecteur dérivé de
est le vecteur dérivé de
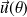 par rapport à
par rapport à
 .
.
Fondamental :
Réduction du domaine d'étude
Si
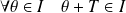 et
et
 , on réduit l'étude à un intervalle de longueur
, on réduit l'étude à un intervalle de longueur
 et on complète la courbe par les rotations de centre
et on complète la courbe par les rotations de centre
 et d'angles
et d'angles
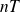 où
où
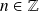 .
.Si
 est un multiple de
est un multiple de
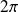 , l'étude d'un intervalle de longueur
, l'étude d'un intervalle de longueur
 suffit pour obtenir toute la courbe.
suffit pour obtenir toute la courbe.Si
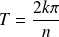 , il suffit d'effectuer
, il suffit d'effectuer
 rotations pour obtenir toute la courbe.
rotations pour obtenir toute la courbe.En particulier si
 , la courbe est symétrique par rapport au point
, la courbe est symétrique par rapport au point
 .
.
Si
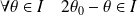 et
et
 , on réduit l'étude à
, on réduit l'étude à
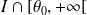 ou
ou
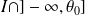 et on complète la courbe par symétrie :
et on complète la courbe par symétrie :par rapport à la droite
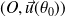 si
si
 .
.par rapport à la droite
 si
si
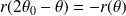 .
.
Dans l'exemple précédent :
La fonction
 est périodique de période
est périodique de période
 .
.Donc on réduit l'étude à
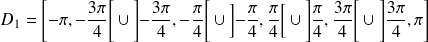 et on obtiendra ainsi toute la courbe.
et on obtiendra ainsi toute la courbe.
La fonction
 est impaire :
est impaire :
 et
et
 .
.Et quand
 décrit
décrit
 , alors
, alors
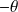 décrit
décrit
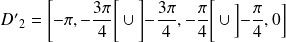 .
.Donc on réduit l'étude à
 et on complètera la courbe par symétrie par rapport à la droite
et on complètera la courbe par symétrie par rapport à la droite
 , donc par rapport à l'axe des ordonnées.
, donc par rapport à l'axe des ordonnées.De plus :
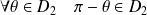 et
et
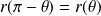 .
.Et quand
 décrit
décrit
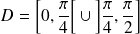 , alors
, alors
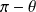 décrit
décrit
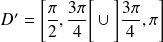 .
.Donc on réduit l'étude à
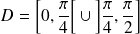 et on complètera la courbe par symétrie par rapport à la droite
et on complètera la courbe par symétrie par rapport à la droite
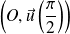 , donc aussi par rapport à l'axe des ordonnées.
, donc aussi par rapport à l'axe des ordonnées.
Remarque : En fait,
 et :
et :
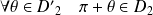 et
et
 , donc :
, donc :
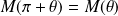 .
.
Donc les arcs de courbe correspondant à
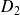 et à
et à
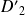 sont confondus.
sont confondus.
Fondamental :
Etude asymptotique
Si
 , la courbe admet un point limite d'affixe
, la courbe admet un point limite d'affixe
 .
.Si
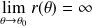 , la courbe admet une direction asymptotique
, la courbe admet une direction asymptotique
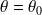 et l'on étudie la limite de
et l'on étudie la limite de
 :
:Si
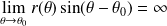 , la courbe admet une branche parabolique de direction
, la courbe admet une branche parabolique de direction
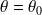 .
.Si
 , la courbe admet une asymptote d'équation
, la courbe admet une asymptote d'équation
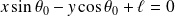 .
.
Si
 tend vers l'infini, on a une spirale :
tend vers l'infini, on a une spirale :Si
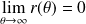 , la spirale admet un point asymptote
, la spirale admet un point asymptote
 .
.Si
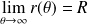 (
(
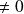 ), la spirale admet un cercle asymptote de centre
), la spirale admet un cercle asymptote de centre
 et de rayon
et de rayon
 .
.Si
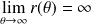 , la spirale s'éloigne à l'infini.
, la spirale s'éloigne à l'infini.
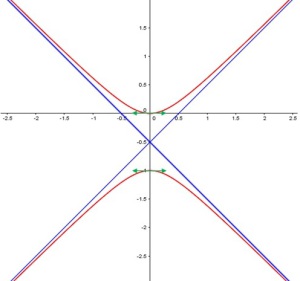
Dans l'exemple précédent :
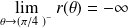 et
et
 . Donc on étudie la limite de
. Donc on étudie la limite de
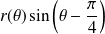 .
.
Or :
 .
.
Donc :
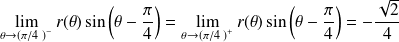 .
.
Donc la courbe admet une asymptote oblique d'équation
 , donc d'équation
, donc d'équation
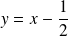 .
.
Méthode :
L'étude des variations de la fonction
 met en évidence les valeurs du paramètre pour lesquels une étude locale est nécessaire.
met en évidence les valeurs du paramètre pour lesquels une étude locale est nécessaire.
On précisera en particulier les valeurs du paramètre pour lesquels la fonction
 s'annule, donc où la courbe passe par le pôle
s'annule, donc où la courbe passe par le pôle
 .
.
Fondamental :
Etude locale en un point autre que le pôle O
Les points autres que le pôle
 sont réguliers, donc ce sont des points ordinaires ou des points d'inflexion.
sont réguliers, donc ce sont des points ordinaires ou des points d'inflexion.La tangente a pour vecteur directeur
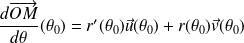 .
.
Etude locale au pôle O
Seul le point
 peut être un point stationnaire, donc c'est un point ordinaire ou un point de rebroussement de première espèce.
peut être un point stationnaire, donc c'est un point ordinaire ou un point de rebroussement de première espèce.La tangente a pour vecteur directeur
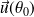 .
.
Dans l'exemple précédent :
On complète ensuite la courbe par symétrie par rapport à l'axe des ordonnées. |
Fondamental :
L'abscisse curviligne d'origine
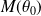 est :
est :
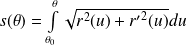 .
.
La courbure au point
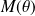 est :
est :
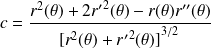 .
.