Exo 10
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
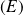l'équation différentielle :
.
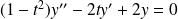On se propose de résoudre cette équation différentielle sur
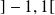par deux méthodes différentes.
Méthode 1 : Recherche des solutions développables en série entière.
Soit
une série entière de rayon de convergence
dont la somme est solution de l'équation différentielle.
Question
Déterminer les coefficients
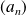en fonction de
.En déduire le rayon de convergence de la série.
Exprimer la somme de la série à l'aide des fonctions usuelles.
En déduire toutes les solutions de
.
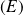Commencez par déterminer une relation de récurrence vérifiée par la suite
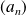pour que sa somme soit solution de
.
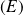Soit
la fonction définie par :
.
A l'intérieur de l'intervalle de convergence,
est indéfiniment dérivable.
et
.
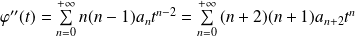Donc :
.
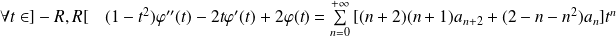Or
est solution de
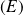. Donc :
.
Donc :
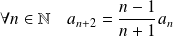. On raisonne par récurrence.
Donc :
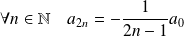et :
.
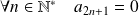Donc :
.
Soit :
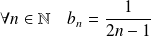. Donc :
.
Donc le rayon de convergence de la série
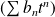est
.
Donc le rayon de convergence de la série
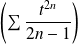est
. Donc :
.
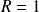Donc
est solution de
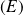si et seulement si :
.
Or :
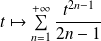est la primitive de :
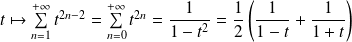qui s'annule en
.
Donc :
.
Donc :
.
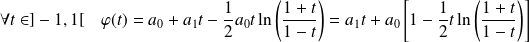Donc les fonctions
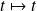et
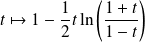sont solutions de
.
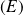Le wronskien :
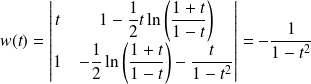ne s'annule pas.
Or
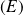est une équation linéaire homogène d'ordre
, donc l'ensemble des solutions est un espace vectoriel de dimension
.
Donc les fonctions
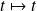et
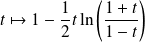forment un système fondamental de solutions.
Conclusion : Les solutions de l'équation
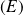sur
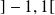sont les fonctions
où
.
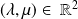Méthode 2 : Abaissement de l'ordre.
On peut remarquer que la fonction
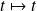est solution évidente de l'équation
.
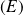Question
On pose :
. Déterminer l'équation différentielle vérifiée par
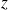.On pose :
. Déterminer l'équation différentielle vérifiée par
.En déduire toutes les solutions de
.
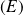On se place sur
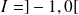ou
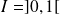et on pose :
.
Donc :
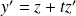, et :
.
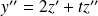Donc l'équation
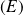équivaut sur
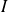à :
.
Donc l'équation devient :
.
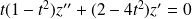On se ramène à une équation du premier ordre en posant :
.
L'équation devient :
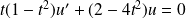, donc :
.
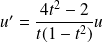Or :
a pour primitive :
.
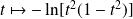Donc
est solution s'il existe
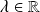tel que :
.
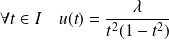Donc :
.
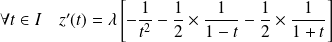Donc :
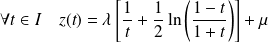avec
.
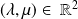Donc :
. Il reste à raccorder en
.
Une fonction
est solution de
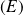si et seulement si elle est de la forme :
.
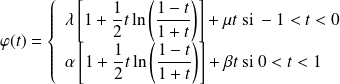Par continuité en
:
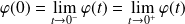. Donc :
.
Par dérivabilité en
:
. Donc :
.
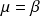On obtient :
qui est dérivable deux fois et vérifie l'équation
.
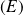Conclusion : Les solutions de l'équation
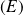sur
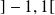sont les fonctions
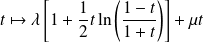où
.
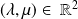On retrouve sous une autre forme les solutions trouvées par la première méthode.
