Exo 9
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
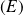 l'équation différentielle :
l'équation différentielle :
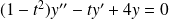 .
.
Question
Résoudre l'équation
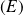 sur l'intervalle
sur l'intervalle
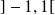 en effectuant le changement de variable :
en effectuant le changement de variable :
 .
.
Déterminez et résolvez l'équation différentielle vérifiée par la fonction :
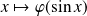 si
si
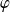 est solution de
est solution de
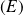 .
.
Si
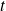 appartient à
appartient à
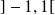 , on pose :
, on pose :
 , donc :
, donc :
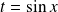 .
.
La fonction
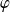 est solution de
est solution de
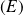 si :
si :
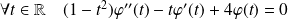 .
.
Donc :
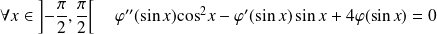 .
.
Soit
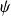 la fonction définie par :
la fonction définie par :
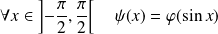 .
.
Donc :
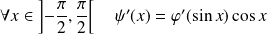 , et :
, et :
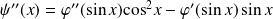 .
.
Donc la fonction
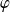 est solution de (E) sur
est solution de (E) sur
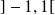 si et seulement si
si et seulement si
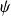 est solution de l'équation :
est solution de l'équation :
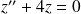 sur
sur
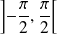 .
.
L'équation caractéristique
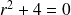 a pour racines :
a pour racines :
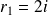 et
et
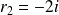 .
.
Donc il existe deux réels
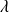 et
et
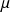 tels que :
tels que :
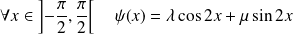 .
.
Or :
 , donc :
, donc :
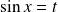 et
et
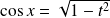 car
car
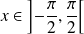 , donc :
, donc :
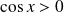 .
.
Donc :
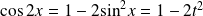 , et :
, et :
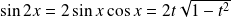 .
.
On obtient :
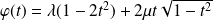 . Et cette fonction vérifie bien l'équation
. Et cette fonction vérifie bien l'équation
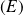 sur
sur
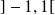 .
.
Conclusion : Les solutions de l'équation
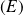 sur
sur
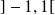 sont les fonctions
sont les fonctions
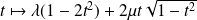 où
où
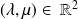 .
.
Question
Résoudre l'équation
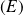 sur l'intervalle
sur l'intervalle
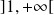 en effectuant le changement de variable :
en effectuant le changement de variable :
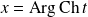 .
.
Déterminez et résolvez l'équation différentielle vérifiée par la fonction :
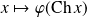 si
si
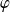 est solution de
est solution de
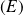 .
.
Si
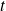 appartient à
appartient à
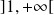 , on pose :
, on pose :
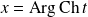 , donc :
, donc :
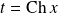 .
.
La fonction
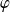 est solution de
est solution de
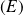 si :
si :
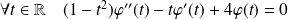 .
.
Donc :
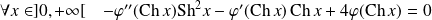 .
.
Soit
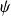 la fonction définie par :
la fonction définie par :
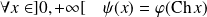 .
.
Donc :
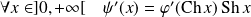 , et :
, et :
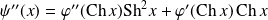 .
.
Donc la fonction
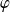 est solution de
est solution de
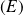 sur
sur
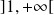 si et seulement si
si et seulement si
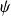 est solution de l'équation :
est solution de l'équation :
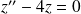 sur
sur
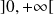 .
.
L'équation caractéristique
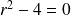 a pour racines :
a pour racines :
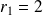 et
et
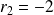 .
.
Donc il existe deux réels
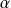 et
et
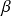 tels que :
tels que :
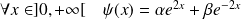 .
.
Or :
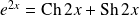 et :
et :
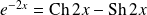 .
.
Donc il existe deux réels
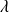 et
et
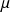 tels que :
tels que :
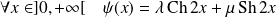 .
.
Or :
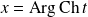 , donc :
, donc :
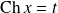 , et :
, et :
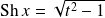 car
car
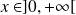 , donc :
, donc :
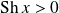 .
.
Donc :
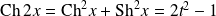 , et :
, et :
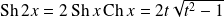 .
.
On obtient :
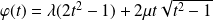 . Et cette fonction vérifie bien l'équation
. Et cette fonction vérifie bien l'équation
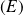 sur
sur
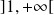 .
.
Conclusion : Les solutions de l'équation
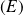 sur
sur
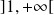 sont les fonctions
sont les fonctions
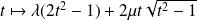 où
où
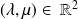 .
.
Question
Résoudre l'équation
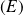 sur l'intervalle
sur l'intervalle
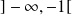 en effectuant le changement de variable :
en effectuant le changement de variable :
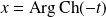 .
.
Déterminez et résolvez l'équation différentielle vérifiée par la fonction :
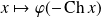 si
si
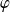 est solution de
est solution de
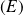 .
.
Le raisonnement est identique sur
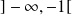 en posant :
en posant :
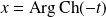 , donc :
, donc :
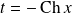 .
.
On définit :
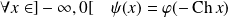 .
.
On montre que la fonction
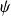 est solution de l'équation :
est solution de l'équation :
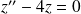 sur
sur
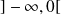 .
.
Conclusion : Les solutions de l'équation
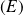 sur
sur
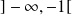 sont les fonctions
sont les fonctions
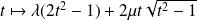 où
où
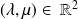 .
.
Remarque :
On pouvait aussi faire le changement de variable
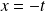 et remarquer que la fonction
et remarquer que la fonction
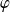 est solution de l'équation sur
est solution de l'équation sur
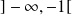 si et seulement si la fonction
si et seulement si la fonction
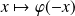 est solution de l'équation sur
est solution de l'équation sur
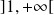 .
.
Question
Résoudre l'équation
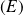 sur
sur
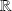 .
.
Etudiez la continuité et la dérivabilité en
 et en
et en
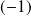 .
.
Si
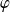 est une solution de l'équation
est une solution de l'équation
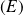 sur
sur
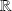 , alors sur les intervalles
, alors sur les intervalles
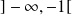 ,
,
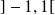 et
et
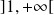 ,
,
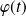 a l'expression trouvée dans les questions précédentes.
a l'expression trouvée dans les questions précédentes.
Donc :
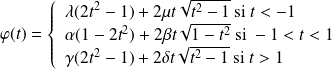 .
.
La fonction
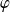 doit être continue et dérivable deux fois sur
doit être continue et dérivable deux fois sur
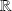 .
.
Donc :
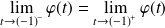 et :
et :
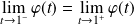 . Donc :
. Donc :
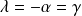 .
.
Et :
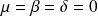 car les fonctions
car les fonctions
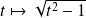 et
et
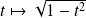 ne sont pas dérivables en
ne sont pas dérivables en
 et en
et en
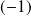 .
.
On obtient donc :
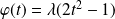 qui est évidemment dérivable deux fois sur
qui est évidemment dérivable deux fois sur
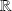 et vérifie l'équation
et vérifie l'équation
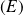 .
.
Conclusion : Les solutions de l'équation
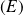 sur
sur
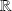 sont les fonctions
sont les fonctions
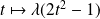 où
où
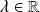 .
.





