Exo 5
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Les trois questions sont indépendantes.
Question
Résoudre sur
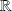l'équation différentielle
:
.
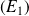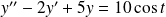Résolvez l'équation homogène, puis cherchez une solution particulière sous la forme :
.
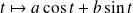Il s'agit d'une équation différentielle linéaire scalaire d'ordre
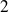à coefficients constants.
Son équation caractéristique :
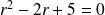a pour racines :
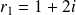et
.
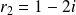Donc les solutions de l'équation homogène associée à
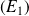sont les fonctions :
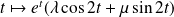où
.
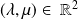On recherche une solution particulière de
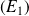de la forme :
.
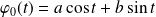Donc :
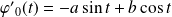, et :
.
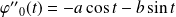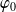est solution de
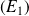si :
.
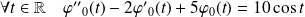Donc :
.
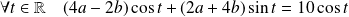On obtient :
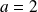et
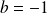. Donc :
.
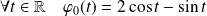Conclusion : Les solutions de l'équation
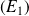sont les fonctions
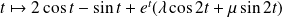où
.
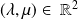Question
Résoudre sur
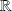l'équation différentielle
:
.
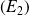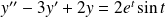Résolvez l'équation homogène, puis cherchez une solution particulière sous la forme :
.
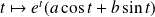Il s'agit d'une équation différentielle linéaire scalaire d'ordre
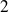à coefficients constants.
Son équation caractéristique :
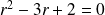a pour racines :
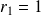et
.
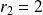Donc les solutions de l'équation homogène associée à
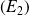sont les fonctions :
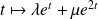où
.
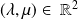On recherche une solution particulière de
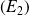de la forme :
.
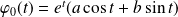Donc :
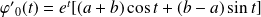, et :
.
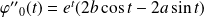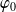est solution de
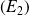si :
.
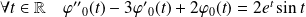Donc :
.
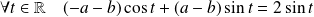On obtient :
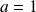et
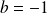. Donc :
.
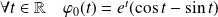Conclusion : Les solutions de l'équation
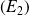sont les fonctions
où
.
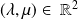Question
Résoudre sur
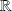l'équation différentielle
:
.
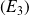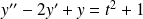Résolvez l'équation homogène, puis cherchez une solution particulière sous forme polynômiale.
Il s'agit d'une équation différentielle linéaire scalaire d'ordre
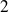à coefficients constants.
Son équation caractéristique :
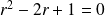a pour racines :
.
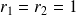Donc les solutions de l'équation homogène associée à
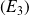sont les fonctions :
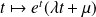où
.
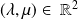On recherche une solution particulière de
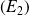sous forme polynômiale.
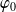est solution de
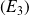si :
.
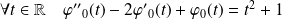Le terme de plus haut degré du premier membre est celui de
.
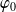Donc
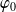est de la forme :
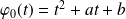. Donc :
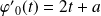, et :
.
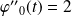Donc :
.
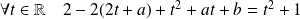On obtient :
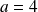et
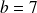. Donc :
.
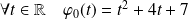Conclusion : Les solutions de l'équation
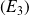sont les fonctions
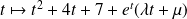où
.
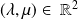