Exo 8
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
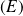l'équation différentielle :
.
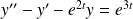Question
Montrer qu'une fonction
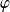est solution de
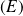si et seulement si la fonction
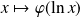est solution d'une équation différentielle que l'on déterminera sur
.
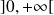Ecrivez l'équation pour
.
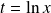Dans l'équation différentielle, on fait le changement de variable :
.
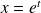La fonction
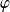est solution de
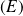si et seulement si :
.
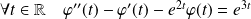Or la fonction
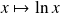est bijective de
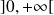dans
.
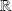Donc
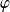est solution si et seulement si :
.
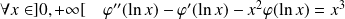Soit
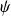la fonction définie par :
.
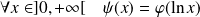Donc :
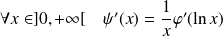, et :
.
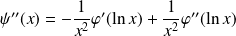Donc :
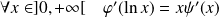et :
.
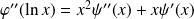Donc
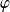est solution de
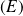si et seulement si :
.
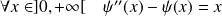Conclusion : Une fonction
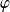est solution de
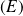si et seulement si la fonction
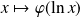est solution de l'équation
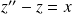sur
.
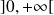Question
En déduire les solutions de
.
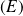Résolvez l'équation :
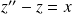pour déterminer
.
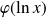L'équation
:
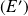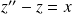est une équation linéaire d'ordre 2 à coefficients constants.
Son équation caractéristique :
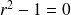a pour racines
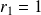et
.
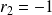Donc les solutions de l'équation différentielle homogène associée sont les fonctions :
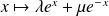où
.
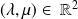Et la fonction :
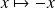est solution évidente de l'équation avec second membre.
Donc les solutions de l'équation
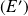sont de la forme :
.
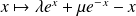Donc
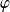est solution de
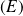si et seulement si :
.
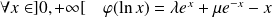Or :
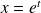. Donc :
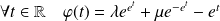avec
.
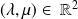Conclusion : Les solutions de l'équation différentielle
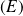sont les fonctions
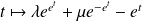où
.
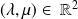