Equations différentielles linéaires scalaires du second ordre
Les fonctions considérées sont des fonctions définies sur un intervalle
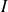 de
de
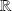 et à valeurs dans
et à valeurs dans
 ou
ou
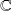 .
.
Définition :
On appelle équation différentielle linéaire scalaire du second ordre toute équation
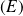 de la forme :
de la forme :
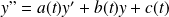 , où
, où
 ,
,
 et
et
 sont des fonctions continues sur
sont des fonctions continues sur
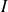 .
.
On appelle équation homogène associée à
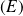 (ou équation sans second membre) l'équation
(ou équation sans second membre) l'équation
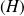 :
:
 .
.
Par exemple, l'équation
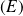 :
:
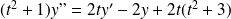 est une équation différentielle linéaire scalaire du second ordre sur
est une équation différentielle linéaire scalaire du second ordre sur
 .
.
En effet, le coefficient
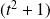 de
de
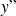 ne s'annule pas. Donc elle équivaut à :
ne s'annule pas. Donc elle équivaut à :
 .
.
Et l'équation homogène associée
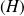 est :
est :
 .
.
Remarque :
Dans le cas où
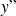 est affecté d'un coefficient qui s'annule, on est amené à résoudre l'équation différentielle sur chaque intervalle où le coefficient est non nul, puis à raccorder les solutions trouvées.
est affecté d'un coefficient qui s'annule, on est amené à résoudre l'équation différentielle sur chaque intervalle où le coefficient est non nul, puis à raccorder les solutions trouvées.
Fondamental :
Propriétés
Soit
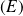 l'équation différentielle
l'équation différentielle
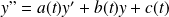 , où
, où
 ,
,
 et
et
 sont des fonctions continues sur
sont des fonctions continues sur
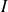 et soit
et soit
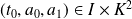 .
.
Toute solution de l'équation différentielle
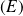 est de classe
est de classe
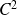 sur
sur
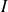 .
.Théorème de Cauchy-Lipschitz : Il existe une unique solution
 de
de
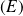 qui vérifie la condition initiale
qui vérifie la condition initiale
 et
et
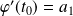 .
.L'ensemble
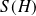 des solutions de l'équation homogène est un espace vectoriel de dimension
des solutions de l'équation homogène est un espace vectoriel de dimension
 .
. Toute base de
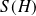 est appelée système fondamental de solutions de
est appelée système fondamental de solutions de
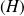 .
.Si
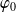 est une solution de l'équation
est une solution de l'équation
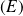 , une fonction
, une fonction
 est solution de
est solution de
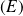 si et seulement si
si et seulement si
 appartient à
appartient à
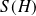 .
.
Pour obtenir un système fondamental de solutions de
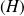 , il faut donc trouver deux solutions
, il faut donc trouver deux solutions
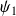 et
et
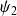 qui forment un système libre dans
qui forment un système libre dans
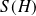 .
.
Fondamental :
On appelle wronskien du couple
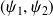 de solutions de
de solutions de
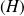 la fonction
la fonction
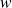 définie par :
définie par :
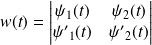 .
.
Le couple
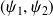 de solutions de
de solutions de
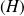 est un système fondamental de solutions de
est un système fondamental de solutions de
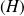 si et seulement si son wronskien n'est pas nul
si et seulement si son wronskien n'est pas nul
Il suffit de trouver
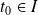 tel que
tel que
 . Alors :
. Alors :
 .
.
Dans l'exemple précédent, on recherche des solutions de l'équation
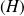 sous forme polynômiale avec un degré
sous forme polynômiale avec un degré
 inconnu.
inconnu.
En raisonnant sur les degrés, on montre que
 ou
ou
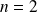 , et on obtient les fonctions définies par :
, et on obtient les fonctions définies par :
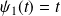 et
et
 .
.
Le wronskien vaut :
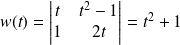 . Donc :
. Donc :
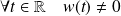 .
.
Donc le couple
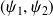 est un système fondamental de solutions de
est un système fondamental de solutions de
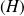 .
.
Donc l'ensemble des solutions de
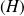 est l'ensemble des fonctions :
est l'ensemble des fonctions :
 où
où
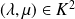 .
.
La fonction
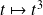 est solution de l'équation
est solution de l'équation
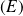 .
.
Donc l'ensemble des solutions de
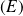 est l'ensemble des fonctions :
est l'ensemble des fonctions :
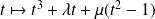 où
où
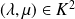 .
.
Fondamental :
Cas où les coefficients sont constants
On associe à
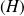 son équation « caractéristique » :
son équation « caractéristique » :
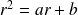 de racines
de racines
 et
et
 dans
dans
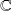 .
.
Si
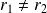 et
et
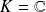 , on peut prendre :
, on peut prendre :
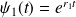 et
et
 .
.Si
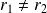 et
et
 , on peut prendre :
, on peut prendre :
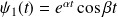 et
et
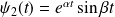 où
où
 et
et
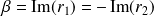 .
.Si
 , on peut prendre
, on peut prendre
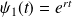 et
et
 .
.
Dans le cas où l'on ne trouve pas une solution particulière évidente de
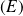 , on utilise la méthode de variation de constante.
, on utilise la méthode de variation de constante.
Méthode :
Méthode de variation de constante
Soit
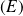 l'équation différentielle
l'équation différentielle
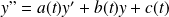 , où
, où
 ,
,
 et
et
 sont des fonctions continues sur l'intervalle
sont des fonctions continues sur l'intervalle
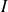 , et
, et
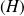 l'équation homogène associée.
l'équation homogène associée.
On détermine un système fondamental
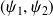 de solutions de l'équation homogène
de solutions de l'équation homogène
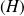 .
.On en déduit la solution générale de l'équation homogène :
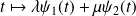 où
où
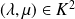 .
.On cherche une solution de l'équation
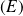 sous la forme :
sous la forme :
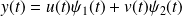 (ce qui revient à faire varier
(ce qui revient à faire varier
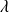 et
et
 ).
).Si les fonctions
 et
et
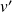 vérifient le système :
vérifient le système :
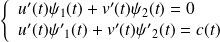 , alors
, alors
 est solution de
est solution de
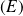 .
.On en déduit les fonctions
 et
et
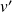 en résolvant le système car son déterminant est le wronskien, donc il est non nul.
en résolvant le système car son déterminant est le wronskien, donc il est non nul.Il suffit de trouver les primitives de ces fonctions pour avoir l'ensemble des solutions de l'équation
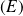 .
.
Dans l'exemple précédent (en supposant que l'on n'a pas trouvé de solution particulière), on pose :
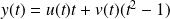 .
.
Les fonctions
 et
et
 vérifient le système :
vérifient le système :
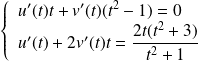 .
.
Donc :
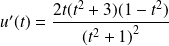 et
et
 .
.
En faisant apparaître les puissances de
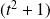 , on remarque que :
, on remarque que :
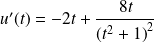 et
et
 .
.
On obtient :
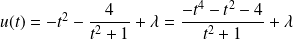 et :
et :
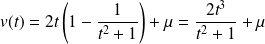 .
.
Donc les solutions de
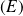 sont de la forme :
sont de la forme :
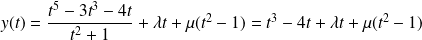 .
.
On retrouve l'ensemble des solutions déjà trouvé puisque :
 avec
avec
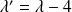 .
.





