Exo 6
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Résoudre sur l'intervalle
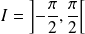l'équation différentielle :
.
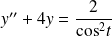Résolvez l'équation homogène, puis utilisez la méthode de variation de constante.
Il s'agit d'une équation différentielle linéaire scalaire d'ordre
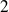à coefficients constants.
Son équation caractéristique :
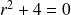a pour racines :
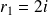et
.
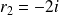Donc les solutions de l'équation homogène sont les fonctions :
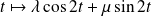où
.
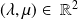On utilise la méthode de variation de constante en posant :
.
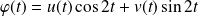Les fonctions
et
vérifient les conditions :
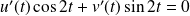, et :
.
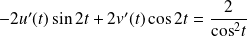On obtient :
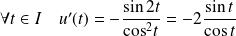, donc :
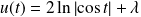où
.
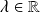Et :
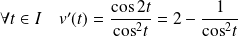, donc :
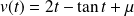où
.
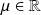Conclusion : Les solutions de l'équation sont les fonctions
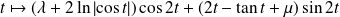où
.
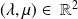