Exo 6
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Les questions suivantes sont indépendantes.
Question
Montrer que l'ensemble des fonctions constantes sur
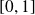 et l'ensemble des fonctions
et l'ensemble des fonctions
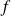 continues telles que
continues telles que
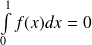 sont deux sous-espaces vectoriels supplémentaires de l'espace vectoriel
sont deux sous-espaces vectoriels supplémentaires de l'espace vectoriel
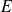 des fonctions continues sur
des fonctions continues sur
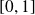 à valeurs réelles.
à valeurs réelles.
Démontrez successivement que
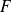 et
et
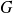 sont des sous-espaces vectoriels, que la somme
sont des sous-espaces vectoriels, que la somme
 est directe et que
est directe et que
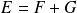 .
.
Soient :
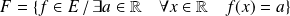 et
et
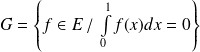 .
.
Montrons successivement que
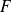 et
et
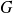 sont des sous-espaces vectoriels, que la somme
sont des sous-espaces vectoriels, que la somme
 est directe et que
est directe et que
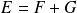 .
.
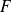 n'est pas vide car la fonction nulle est constante sur
n'est pas vide car la fonction nulle est constante sur
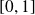 .
.Soient
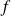 et
et
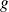 deux éléments de
deux éléments de
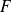 et
et
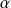 un réel.
un réel.Donc :
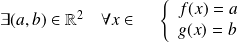 .
.Donc :
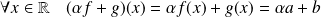 . Donc :
. Donc :
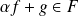 .
.Donc
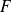 est un sous-espace vectoriel de
est un sous-espace vectoriel de
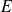 .
.
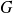 n'est pas vide car la fonction nulle vérifie :
n'est pas vide car la fonction nulle vérifie :
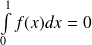 .
.Soient
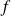 et
et
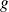 deux éléments de
deux éléments de
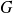 et
et
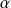 un réel. Donc :
un réel. Donc :
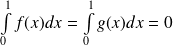 .
.Donc :
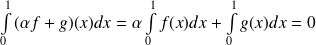 . Donc :
. Donc :
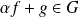 .
.Donc
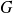 est un sous-espace vectoriel de
est un sous-espace vectoriel de
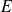 .
.
Soit
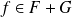 . Donc :
. Donc :
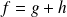 avec
avec
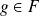 et
et
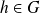 .
.Donc :
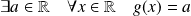 et
et
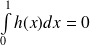 .
.Donc :
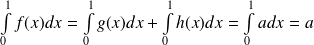 . Donc
. Donc
 est unique.
est unique.Or :
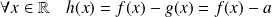 .
.Donc, pour tout
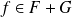 , les fonctions
, les fonctions
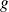 et
et
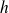 sont uniques.
sont uniques.Donc la somme
 est directe.
est directe.
Soit
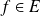 . On pose :
. On pose :
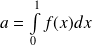 , puis
, puis
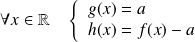 .
.Les fonctions
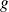 et
et
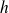 sont continues et il est évident que
sont continues et il est évident que
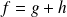 et que
et que
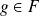 .
.De plus :
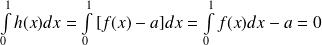 . Donc :
. Donc :
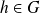 .
.Donc :
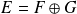 .
.
Conclusion :
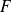 et
et
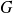 sont deux sous-espaces supplémentaires de
sont deux sous-espaces supplémentaires de
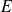 .
.
Question
Montrer que l'ensemble des suites réelles
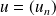 telles que
telles que
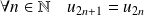 et l'ensemble des suites réelles
et l'ensemble des suites réelles
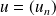 telles que
telles que
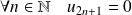 sont deux sous-espaces vectoriels supplémentaires de l'espace vectoriel
sont deux sous-espaces vectoriels supplémentaires de l'espace vectoriel
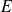 des suites réelles.
des suites réelles.
Démontrez successivement que
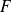 et
et
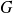 sont des sous-espaces vectoriels, que la somme
sont des sous-espaces vectoriels, que la somme
 est directe et que
est directe et que
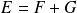 .
.
Soient :
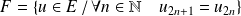 et
et
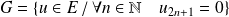 .
.
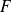 n'est pas vide car la suite nulle vérifie :
n'est pas vide car la suite nulle vérifie :
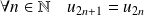 .
.Soient
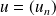 et
et
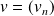 deux éléments de
deux éléments de
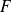 et
et
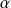 un réel.
un réel.Donc :
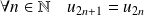 et
et
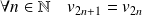 .
.La suite
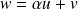 a pour terme général :
a pour terme général :
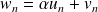 .
.Donc :
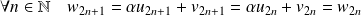 . Donc :
. Donc :
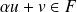 .
.Donc
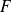 est un sous-espace vectoriel de
est un sous-espace vectoriel de
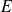 .
.
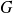 n'est pas vide car la suite nulle vérifie :
n'est pas vide car la suite nulle vérifie :
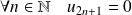 .
.Soient
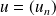 et
et
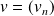 deux éléments de
deux éléments de
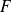 et
et
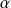 un réel.
un réel.Donc :
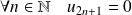 et
et
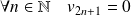 .
.La suite
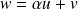 a pour terme général :
a pour terme général :
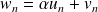 .
.Donc :
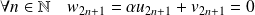 . Donc :
. Donc :
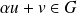 .
.Donc
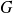 est un sous-espace vectoriel de
est un sous-espace vectoriel de
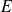 .
.
Soit
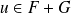 . Donc :
. Donc :
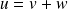 avec
avec
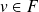 et
et
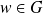 .
.Donc :
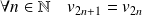 et
et
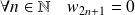 .
.Or :
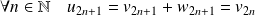 et
et
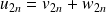 .
.Donc :
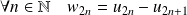 et
et
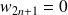 . Et
. Et
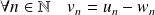 .
.Donc, pour tout
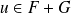 , les suites
, les suites
 et
et
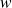 sont uniques.
sont uniques.Donc la somme
 est directe.
est directe.
Soit
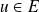 . On pose :
. On pose :
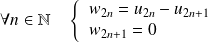 et
et
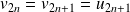 .
.On définit ainsi deux suites
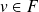 et
et
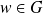 .
.De plus :
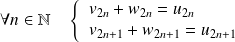 . Donc :
. Donc :
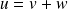 .
.Donc :
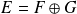 .
.
Conclusion :
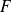 et
et
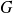 sont deux sous-espaces supplémentaires de
sont deux sous-espaces supplémentaires de
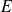 .
.





