Introduction
Prérequis : Cours de spécialité mathématiques sur les similitudes directes et la définition d'une similitude indirecte.
Durée : 90 minutes
Niveau : facile
Énoncé de l'exercice :
Le plan est rapporté au repère orthonormé direct ![]() .
.
Notations :
Si
 est une transformation du plan, on note
est une transformation du plan, on note
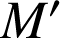 le point d'affixe
le point d'affixe
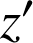 , image par
, image par
 du point
du point
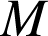 d'affixe
d'affixe
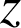 .
.
Il s'agit dans cette partie de (re)démontrer des résultats du cours et plus particulièrement :
«
 est une similitude indirecte si et seulement si son écriture complexe est de la forme
est une similitude indirecte si et seulement si son écriture complexe est de la forme ![]() où
où ![]() . »
. »
1) Caractériser la transformation ![]() dont l'écriture complexe est
dont l'écriture complexe est ![]() .
.
![]() Observez l'image
Observez l'image
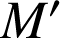 de
de
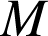 par la transformation (Cabri Java - env. 150Ko)
par la transformation (Cabri Java - env. 150Ko)
Rappel du cours sur le conjugué d'un nombre complexe :
Le conjugué du nombre complexe
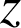 de forme algébrique
de forme algébrique ![]() est
est ![]() .
.
Si
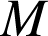 et
et
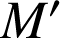 ont pour affixes
ont pour affixes
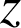 et
et ![]() alors
alors
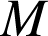 et
et
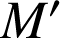 sont symétriques par rapport à l'axe réel.
sont symétriques par rapport à l'axe réel.
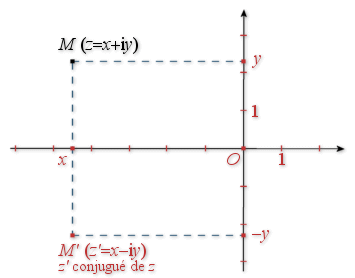
1) Les points ![]() et
et ![]() sont symétriques par rapport à l'axe des abscisses donc la transformation
sont symétriques par rapport à l'axe des abscisses donc la transformation ![]() est la symétrie axiale par rapport à l'axe des abscisses.
est la symétrie axiale par rapport à l'axe des abscisses.
2) Soit
 la transformation dont l'écriture complexe est
la transformation dont l'écriture complexe est ![]() où
où ![]() .
.
Montrer que
 est une similitude indirecte et déterminer son rapport en fonction de
est une similitude indirecte et déterminer son rapport en fonction de
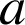 .
.
Décomposer
 à l'aide de
à l'aide de ![]() .
.
![]()
Rappel du cours sur la composée de similitudes :
La composée de
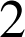 similitudes du plan de rapport
similitudes du plan de rapport
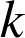 et
et
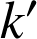 est une similitude du plan de rapport
est une similitude du plan de rapport
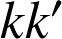 .
.
Cette composée n'est pas commutative.
Plus particulièrement, la composée de
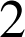 isométries est une isométrie.
isométries est une isométrie.
La composée de deux similitudes directes est directe.
La composée de deux similitudes indirectes est directe.
La composée d'une similitude directe et d'une similitude indirecte est indirecte.
2) ![]() donc
donc
 est la composée de la symétrie
est la composée de la symétrie ![]() suivie de la transformation
suivie de la transformation
 dont l'écriture complexe est
dont l'écriture complexe est
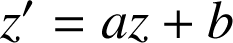 qui est une similitude directe.
qui est une similitude directe.
 est la composée d'une similitude indirecte et d'une similitude directe donc
est la composée d'une similitude indirecte et d'une similitude directe donc
 est une similitude indirecte.
est une similitude indirecte.
Le rapport de la composée de similitudes est le produit des rapports : ![]() est une isométrie donc son rapport est
est une isométrie donc son rapport est
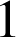 , le rapport de
, le rapport de
 est
est ![]() .
.
 est une similitude indirecte de rapport
est une similitude indirecte de rapport ![]() .
.
3) Soit
 une similitude indirecte et
une similitude indirecte et ![]() la symétrie par rapport à l'axe des abscisses. Montrer que l'écriture complexe de
la symétrie par rapport à l'axe des abscisses. Montrer que l'écriture complexe de ![]() est
est ![]() où
où ![]() .
.
En déduire l'expression complexe de
 .
.
Quelle est la composée de deux similitudes indirectes ?
Si
 ,
,
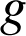 et
et
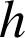 sont trois transformations telles que
sont trois transformations telles que ![]() alors
alors ![]() .
.
Rappel du cours sur la composée de similitudes :
La composée de
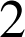 similitudes du plan de rapport
similitudes du plan de rapport
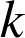 et
et
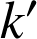 est une similitude du plan de rapport
est une similitude du plan de rapport
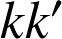 .
.
Cette composée n'est pas commutative.
Plus particulièrement, la composée de
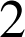 isométries est une isométrie.
isométries est une isométrie.
La composée de deux similitudes directes est directe.
La composée de deux similitudes indirectes est directe.
La composée d'une similitude directe et d'une similitude indirecte est indirecte.
Que vaut ![]() ? Qui est
? Qui est ![]() ?
?
3)
 est une similitude indirecte et
est une similitude indirecte et ![]() aussi donc
aussi donc ![]() est une similitude directe
est une similitude directe
 qui a, d'après le cours, pour écriture complexe :
qui a, d'après le cours, pour écriture complexe :
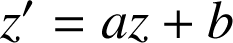 .
.
Donc ![]() , d'où
, d'où ![]() .
.
![]() est la transformation identique et
est la transformation identique et ![]() puisque
puisque ![]() , donc
, donc ![]() .
.
L'écriture complexe de ![]() est :
est : ![]() ,
,
l'écriture complexe de
 est :
est :
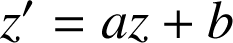 ,
,
donc l'écriture complexe de
 est
est ![]() .
.
4) Caractériser les similitudes indirectes par leur forme complexe.
Relire les résultats des questions 2) et 3).
4) D'après la question 2), si
 est une similitude indirecte, alors son écriture complexe est
est une similitude indirecte, alors son écriture complexe est ![]() et son rapport est
et son rapport est ![]() .
.
D'après la question 3), si l'écriture complexe de
 est
est ![]() , alors
, alors
 est une similitude indirecte.
est une similitude indirecte.
Donc :
 est une similitude indirecte si et seulement si son écriture complexe est
est une similitude indirecte si et seulement si son écriture complexe est ![]() (son rapport est
(son rapport est ![]() ).
).
5) Dans quel cas l'écriture ![]() où
où ![]() est-elle la forme complexe d'une isométrie ?
est-elle la forme complexe d'une isométrie ?
Une isométrie est une similitude particulière.
5) L'écriture complexe ![]() est celle d'une similitude indirecte de rapport
est celle d'une similitude indirecte de rapport ![]() ; elle est une isométrie si et seulement si
; elle est une isométrie si et seulement si ![]() si et seulement si
si et seulement si ![]() .
.
Étude de la similitude indirecte
 d'écriture complexe :
d'écriture complexe : ![]()
1) Quels sont les points invariants par
 ?
?
 peut-elle être une symétrie axiale ?
peut-elle être une symétrie axiale ?
Un point
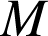 est invariant par une transformation
est invariant par une transformation
 du plan si et seulement si
du plan si et seulement si ![]() .
.
Un point
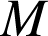 d'affixe
d'affixe ![]() est invariant si et seulement si
est invariant si et seulement si ![]() .
.
1) Le point
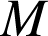 d'affixe
d'affixe
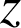 est invariant si et seulement si
est invariant si et seulement si ![]() si et seulement si
si et seulement si ![]() .
.
Soit ![]() avec
avec ![]() ; on obtient :
; on obtient :
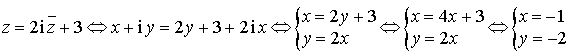
 admet un seul point invariant : le point de coordonnées
admet un seul point invariant : le point de coordonnées ![]() .
.
Une symétrie axiale ayant une infinité de points invariants,
 n'est pas une symétrie axiale.
n'est pas une symétrie axiale.
De plus, le rapport de
 étant
étant ![]() ,
,
 n'est pas une isométrie.
n'est pas une isométrie.
2) Soit
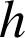 l'homothétie de rapport
l'homothétie de rapport
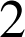 et de centre le point
et de centre le point ![]() d'affixe
d'affixe ![]() .
.
a. Donner l'écriture complexe de ![]() .
.
b. Déterminer l'ensemble des points invariants par ![]() .
.
c. Caractériser
 .
.
a.
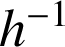 est la réciproque de l'homothétie
est la réciproque de l'homothétie ![]() ; les éléments caractéristiques de
; les éléments caractéristiques de
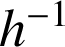 sont donc connus.
sont donc connus.
b. Résoudre
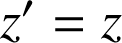 comme au 1).
comme au 1).
c. Trouver les éléments caractéristiques de ![]() .
.
a.
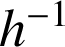 est l'homothétie de centre
est l'homothétie de centre ![]() et de rapport
et de rapport
 .
.
c. Que dire d'une similitude qui a au moins deux points invariants ?
2) a.
Soit ![]() l'image de
l'image de ![]() par
par
 et
et ![]() l'image de
l'image de ![]() par
par
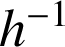 et
et ![]() .
.
On a ![]() .
.
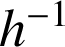 est l'homothétie de centre
est l'homothétie de centre ![]() et de rapport
et de rapport
 donc
donc ![]() .
.
D'où :
L'écriture complexe de ![]() est
est ![]() .
.
2) b.
![]() est invariant par
est invariant par ![]() si et seulement si :
si et seulement si :
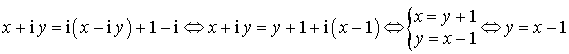
L'ensemble des points invariants par ![]() est la droite
est la droite
 d'équation
d'équation
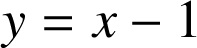 .
.
2) c.
![]() est une similitude qui a une infinité de points invariants, c'est donc l'identité ou une symétrie axiale.
est une similitude qui a une infinité de points invariants, c'est donc l'identité ou une symétrie axiale.
Comme ![]() est une similitude indirecte, d'après son écriture complexe du 2.a),
est une similitude indirecte, d'après son écriture complexe du 2.a), ![]() est la symétrie axiale par rapport à la droite
est la symétrie axiale par rapport à la droite
 d'équation
d'équation
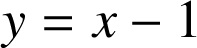 . On la note
. On la note ![]() .
.
Donc ![]() alors :
alors : ![]() donc
donc
 est la composée de l'homothétie de centre
est la composée de l'homothétie de centre ![]() et de rapport
et de rapport
 et de la symétrie axiale par rapport à la droite
et de la symétrie axiale par rapport à la droite
 d'équation
d'équation
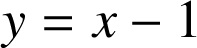 .
.
On remarque que ![]() et il est facile de vérifier :
et il est facile de vérifier : ![]() .
.
![]() Observez les images de
Observez les images de
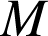 par
par
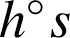 et
et
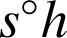 (Java - env. 150Ko)
(Java - env. 150Ko)
Étude de la similitude indirecte
 d'écriture complexe :
d'écriture complexe : ![]()
1) Rechercher les points invariants par
 . Que peut-on en conclure ?
. Que peut-on en conclure ?
Un point
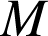 est invariant par une transformation
est invariant par une transformation
 du plan si et seulement si
du plan si et seulement si ![]() .
.
Un point
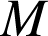 d'affixe
d'affixe ![]() est invariant si et seulement si
est invariant si et seulement si ![]() .
.
1) Le point
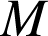 d'affixe
d'affixe
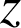 est invariant si et seulement si
est invariant si et seulement si
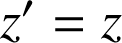 si et seulement si
si et seulement si ![]() .
.
Soit ![]() avec
avec ![]() :
:
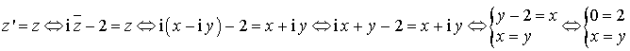
Donc
 n'a pas de point invariant. Mais
n'a pas de point invariant. Mais ![]() donc
donc
 est un antidéplacement qui n'a pas de point invariant, ce n'est pas une symétrie axiale.
est un antidéplacement qui n'a pas de point invariant, ce n'est pas une symétrie axiale.
2) Soit
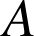 l'image de
l'image de
 par
par ![]() et
et
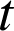 la translation de vecteur
la translation de vecteur ![]() .
.
Déterminer l'écriture complexe de ![]() .
.
Trouver l'affixe de
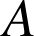 ; quelle est l'écriture complexe d'une translation ?
; quelle est l'écriture complexe d'une translation ?
Rappel du cours sur l'écriture complexe d'une translation :
Au point
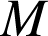 d'affixe
d'affixe
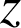 , on associe par la transformation
, on associe par la transformation
 le point
le point
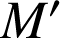 d'affixe
d'affixe
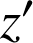 . Dans le cas où
. Dans le cas où
 est une translation de vecteur d'affixe
est une translation de vecteur d'affixe
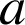 , on a la relation :
, on a la relation :
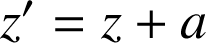 (
(
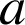 complexe).
complexe).
Quelle est la translation réciproque de ![]() ?
?
2) ![]() donc
donc ![]() et
et ![]() donc
donc ![]() .
.
Le vecteur ![]() a pour affixe
a pour affixe ![]() .
.
![]() est la translation de vecteur
est la translation de vecteur ![]() d'affixe
d'affixe ![]() . Soit
. Soit ![]() l'image de
l'image de ![]() par
par ![]() et
et ![]() l'image de
l'image de ![]() par
par
 alors :
alors :
![]() et
et ![]() .
.
L'écriture complexe de
 est
est ![]() .
.
3) Étudier les points invariants par
 puis en déduire la nature de
puis en déduire la nature de
 .
.
Procéder comme au 1).
3) Le point
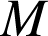 d'affixe
d'affixe
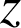 est invariant par
est invariant par
 si et seulement si
si et seulement si ![]() .
.
Soit ![]() avec
avec ![]() :
:
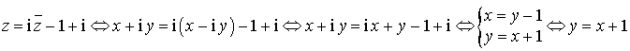
L'ensemble des points invariants de
 est la droite d'équation
est la droite d'équation
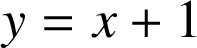 .
.
 est la composée d'une similitude indirecte
est la composée d'une similitude indirecte
 et d'une similitude directe
et d'une similitude directe ![]() donc
donc
 est une similitude indirecte. Ayant plus de deux points invariants,
est une similitude indirecte. Ayant plus de deux points invariants,
 est la symétrie axiale par rapport à la droite
est la symétrie axiale par rapport à la droite
 d'équation
d'équation
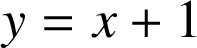 .
.
4) Prouver que
 est la composée d'une symétrie axiale et d'une translation dont le vecteur est un vecteur directeur de l'axe de la symétrie.
est la composée d'une symétrie axiale et d'une translation dont le vecteur est un vecteur directeur de l'axe de la symétrie.
Si ![]() alors
alors ![]() .
.
4) On sait ![]() donc
donc ![]() .
.
 est la composée de la translation de vecteur
est la composée de la translation de vecteur 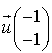 et de la symétrie axiale par rapport à la droite
et de la symétrie axiale par rapport à la droite
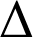 d'équation
d'équation
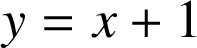 , dont un vecteur directeur est bien
, dont un vecteur directeur est bien 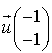 .
.
 est appelée : symétrie glissée d'axe
est appelée : symétrie glissée d'axe
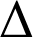 et il est facile de vérifier :
et il est facile de vérifier : ![]() .
.
![]() Observez les images de
Observez les images de
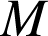 par
par
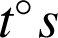 et
et
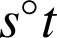 (Java - env. 150Ko)
(Java - env. 150Ko)






