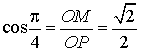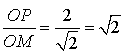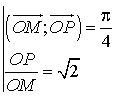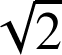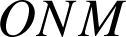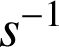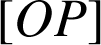Introduction
Prérequis : Cours de spécialité mathématiques sur les similitudes directes.
Durée : 90 minutes
Niveau : très progressif : de facile à difficile
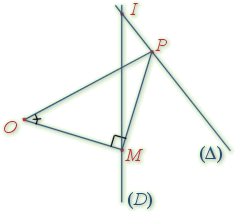
Énoncé de l'exercice
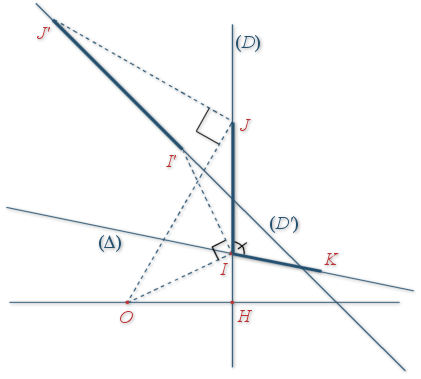
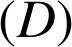et
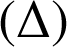sont deux droites sécantes en
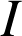et
un point n'appartenant 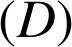ni à
ni à
.
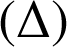On se propose de construire, si cela est possible, un point
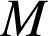sur
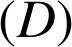et un point
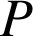sur
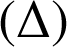tel que le triangle
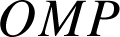soit rectangle isocèle direct en
.
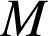1) Analyse
a. Montrer que si le triangle
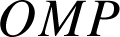est une solution alors
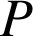est l'image de
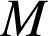par une similitude
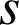à préciser.
b. En déduire, si la construction est possible, la position de
.
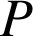2) Synthèse
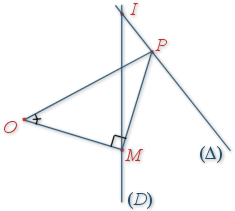
Soit
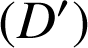l'image de
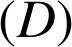par
.
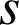a. Montrer que si
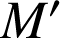est un point de
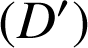et si 
alors le triangle
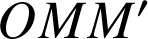est isocèle rectangle et direct en
.
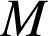b. Décrire la construction de
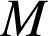et de
.
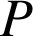3) Discussion
a. Étudier le cas où
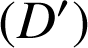et
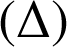sont sécantes. Combien le problème a-t-il de solutions ?
b. Étudier le cas où
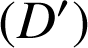et
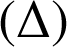sont disjointes.
c. Étudier le cas où
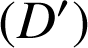et
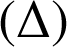sont confondues.
4) Approfondissement
Soit
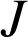un point de
,
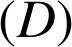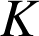un point de
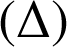tous deux distincts de
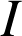. On désigne par
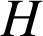le projeté orthogonal de
sur
.
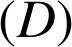On pose 
, 
et 
.
a. Montrer que le problème a une solution unique si et seulement si 
.
b. Montrer que si 
et si le triangle
est rectangle isocèle en
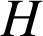alors le problème a une infinité de solutions.
c. Dans quel cas le problème n'a-t-il pas de solution ?
