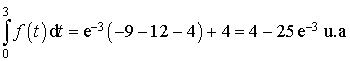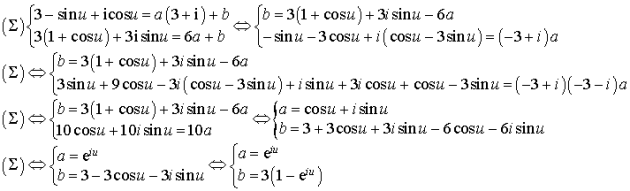Introduction
Prérequis : Cours de spécialité mathématiques sur les similitudes directes et le calcul intégral.
Durée : 90 minutes
Niveau : moyen
Le plan est rapporté au repère orthonormé direct ![]() .
.
Soit
 le point d'affixe
le point d'affixe ![]() et
et
 d'affixe
d'affixe
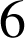 . Pour tout réel
. Pour tout réel
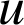 , on considère les deux points
, on considère les deux points
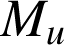 d'affixe
d'affixe ![]() et
et
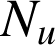 d'affixe
d'affixe ![]() .
.
1) Montrer qu'il existe une unique similitude directe
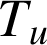 telle que
telle que ![]() et
et ![]() .
.
Que dit le cours sur l'existence d'une similitude transformant deux points
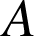 et
et
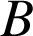 en deux points
en deux points
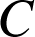 et
et
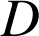 ?
?
Rechercher s'il existe des valeurs de
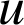 pour lesquelles
pour lesquelles ![]() .
.
1) Les points
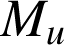 et
et
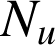 sont confondus si et seulement si :
sont confondus si et seulement si :
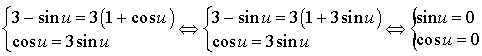
Ce dernier système n'a pas de solution.
Donc pour tout réel
 les points
les points
 et
et
 sont distincts ainsi que
sont distincts ainsi que
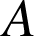 et
et
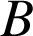 ; il existe donc une unique similitude directe transformant
; il existe donc une unique similitude directe transformant
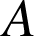 en
en
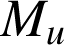 et
et
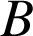 en
en
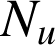 .
.
2) Donner l'écriture complexe de
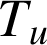 puis préciser les éléments caractéristiques de
puis préciser les éléments caractéristiques de
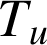 .
.
Quelle est la forme générale de l'écriture complexe d'une similitude directe ?
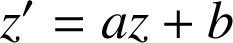
Écrire le système vérifié par
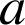 et
et
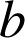 sachant que
sachant que
 et
et
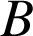 se transforment en
se transforment en
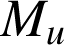 et
et
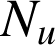 .
.
2) L'écriture complexe de
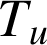 est
est
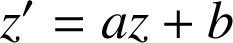 où
où
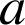 et
et
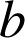 sont deux complexes et
sont deux complexes et
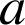 non nul.
non nul.
![]() , donc
, donc ![]() et
et ![]() , donc
, donc ![]() .
.
D'où le système :
L'écriture complexe de
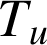 est
est ![]() .
.
Déterminons les points invariants par
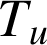 :
: ![]()
Si
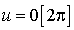 , alors
, alors 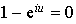 , donc tous les points sont invariants et
, donc tous les points sont invariants et
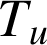 est l'identité du plan.
est l'identité du plan.Si
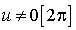 , alors
, alors 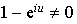 et l'unique point invariant de
et l'unique point invariant de
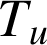 a pour affixe
a pour affixe
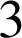 .
.
Dans les deux cas,
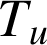 est la rotation d'angle
est la rotation d'angle
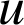 et de centre le point
et de centre le point ![]() d'affixe
d'affixe
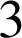 .
.
3) Soit
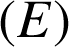 l'ensemble des transformations
l'ensemble des transformations
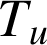 pour
pour
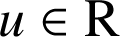 .
.
 contient-il la transformation identique ? Montrer que, pour tout
contient-il la transformation identique ? Montrer que, pour tout
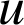 et
et
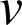 de
de
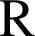 ,
, ![]() et
et ![]() sont des éléments de
sont des éléments de
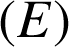 et que
et que ![]() .
.
Revoir le cours sur la composition de similitudes directes de même centre et la transformation réciproque d'une similitude directe.
3) La transformation identique est la rotation d'angle nul, c'est ![]() qui appartient à
qui appartient à
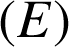 .
.
![]() est la rotation de centre
est la rotation de centre ![]() et d'angle
et d'angle
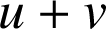 donc
donc ![]() appartient à
appartient à
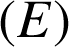 .
.
![]() est la rotation de centre
est la rotation de centre ![]() et d'angle
et d'angle
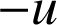 donc
donc ![]() appartient à
appartient à
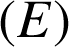 .
.
Un ensemble ayant les propriétés précédentes est dit avoir une structure de groupe. Par exemple l'ensemble des similitudes est un groupe ; de même l'ensemble des translations. L'ensemble des homothéties n'est pas un groupe puisque la composée de deux homothéties de centres différents et de rapports inverses est une translation).
![]()
4) On pose ![]() ,
, 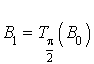 et pour tout entier naturel
et pour tout entier naturel
 non nul :
non nul : 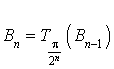 .
.
a. Montrer par récurrence : 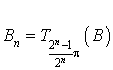 pour tout entier naturel
pour tout entier naturel
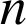 .
.
b. Calculer les coordonnées du point ![]() en fonction de
en fonction de
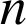 et étudier la position limite des points
et étudier la position limite des points ![]() quand
quand
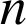 tend vers
tend vers
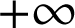 .
.
a. Appliquer ![]() avec
avec ![]() et
et 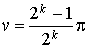 où
où
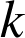 est dans
est dans
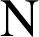 .
.
b. Utiliser la forme complexe de
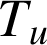 avec
avec 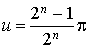 pour calculer l'affixe de
pour calculer l'affixe de
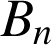 .
.
Puis appliquer le théorème sur la composition des limites d'une fonction et d'une suite.
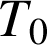 est l'identité donc
est l'identité donc 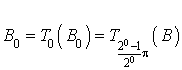 donc la propriété
donc la propriété 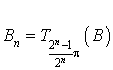 est vraie au rang
est vraie au rang
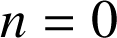 .
.
Soit
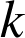 un entier naturel; supposons
un entier naturel; supposons 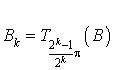 . Alors :
. Alors :
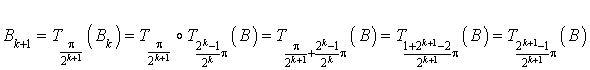
Donc la propriété est héréditaire et comme elle est vraie au rang
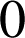 , elle est vraie pour tout entier
, elle est vraie pour tout entier
 .
.
L'écriture complexe de ![]() est
est 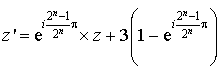 .
.
Si
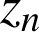 désigne l'affixe de
désigne l'affixe de
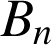 alors, puisque
alors, puisque 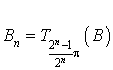 :
:
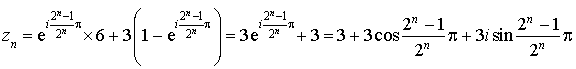
Donc : 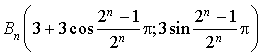 .
.
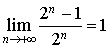 et
et ![]() ; par composition des limites :
; par composition des limites : 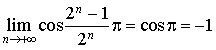 .
.
De même : ![]() donc :
donc : 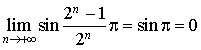 .
.
Donc : 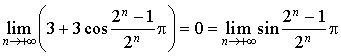 . La suite des points
. La suite des points
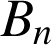 tend vers l'origine.
tend vers l'origine.
Soit
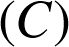 l'ensemble des points
l'ensemble des points ![]() tels que
tels que ![]() et on désigne par
et on désigne par
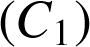 l'image de
l'image de
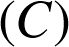 par
par ![]() .
.
1) Montrer que
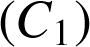 a pour équation
a pour équation ![]() .
.
Désigner par ![]() l'image de
l'image de ![]() par
par
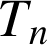 .
.
Utiliser l'écriture complexe de ![]() pour exprimer
pour exprimer
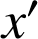 et
et
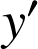 en fonction de
en fonction de
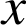 et de
et de
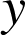 .
.
1) D'après la deuxième question de la partie I, l'écriture complexe de ![]() est :
est : 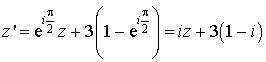 .
.
Si on désigne par ![]() l'image de
l'image de ![]() par
par ![]() alors :
alors :
![]()
donc 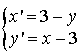 ou
ou 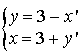
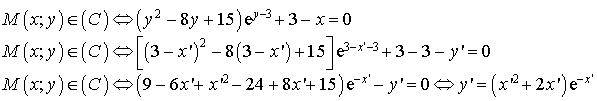
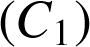 est l'ensemble des points dont les coordonnées
est l'ensemble des points dont les coordonnées ![]() vérifient :
vérifient : ![]() .
.
Donc
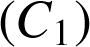 a pour équation
a pour équation ![]() .
.
2) A l'aide de deux intégrations par parties, calculer 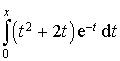 .
.
Penser à vérifier les conditions sur les fonctions
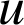 et
et
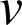 dans la formule d'intégration par parties.
dans la formule d'intégration par parties.
2) Soit
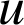 et
et
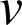 les fonctions définies par
les fonctions définies par ![]() et
et ![]() ;
;
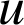 et
et
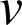 sont dérivables sur
sont dérivables sur
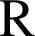 ;
; ![]() et
et ![]() ;
;
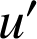 et
et
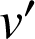 sont continues sur
sont continues sur
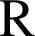 donc d'après le théorème d'intégration par parties :
donc d'après le théorème d'intégration par parties :
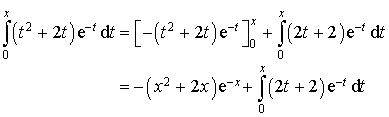
De la même façon :
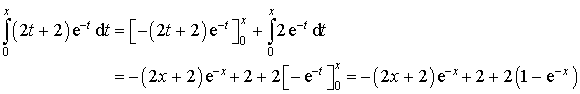
Donc :
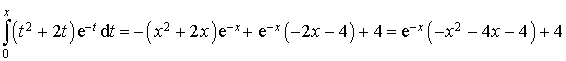
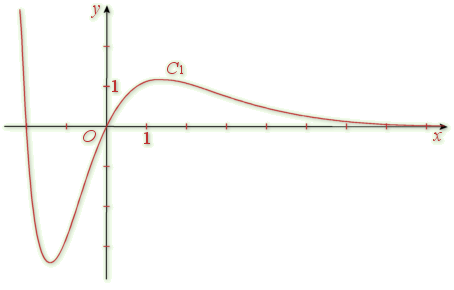
3) A l'aide d'une calculatrice graphique, tracer l'allure de
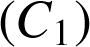 courbe représentative de
courbe représentative de ![]() et en déduire le tracé de
et en déduire le tracé de
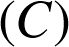 dans le même repère.
dans le même repère.
La calculatrice donne la courbe
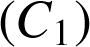 image de
image de
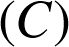 par
par ![]() , comment retrouver
, comment retrouver
 ?
?
![]() Observez l'image
Observez l'image
 de
de
 par la similitude (Cabri Java - env. 150Ko)
par la similitude (Cabri Java - env. 150Ko)
3) ![]() Observez l'image
Observez l'image
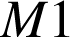 de
de
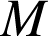 par la similitude (Cabri Java - env. 150Ko)
par la similitude (Cabri Java - env. 150Ko)
4) Calculer l'aire du domaine limité par
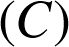 , l'axe des abscisses et les droites d'équations respectives :
, l'axe des abscisses et les droites d'équations respectives :
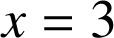 et
et
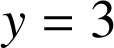 .
.
Une isométrie conserve les aires.
4) 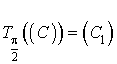 donc
donc 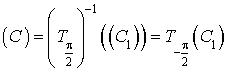 , c'est-à-dire que
, c'est-à-dire que
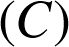 est l'image de
est l'image de
 par la rotation de centre
par la rotation de centre ![]() et d'angle
et d'angle ![]() .
.
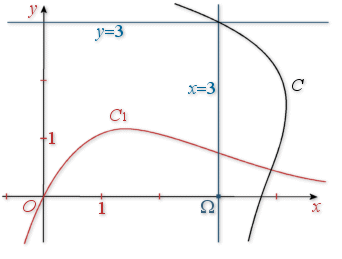
La droite d'équation
 passe par
passe par ![]() , son image par
, son image par ![]() est une droite perpendiculaire passant par
est une droite perpendiculaire passant par ![]() qui est donc l'axe des abscisses.
qui est donc l'axe des abscisses.
De la même façon la droite d'équation
 a pour image l'axe des abscisses et l'axe des abscisses a pour image la droite d'équation
a pour image l'axe des abscisses et l'axe des abscisses a pour image la droite d'équation
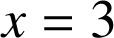 .
.
Le domaine délimité par
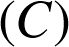 , l'axe des abscisses et les droites d'équations respectives
, l'axe des abscisses et les droites d'équations respectives
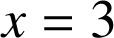 et
et
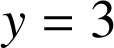 a pour image par
a pour image par ![]() le domaine limité par
le domaine limité par
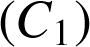 , l'axe des abscisses, l'axe des ordonnées et la droite d'équation
, l'axe des abscisses, l'axe des ordonnées et la droite d'équation
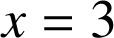 .
. ![]() étant une isométrie, ces deux domaines ont la même aire ; la fonction
étant une isométrie, ces deux domaines ont la même aire ; la fonction
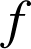 est de façon évidente positive sur
est de façon évidente positive sur
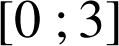 , cette aire est :
, cette aire est :