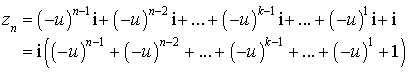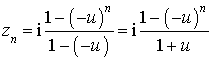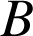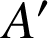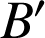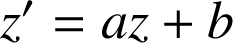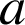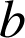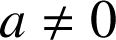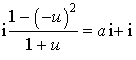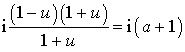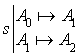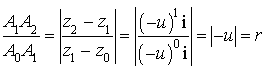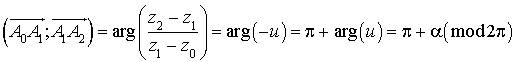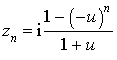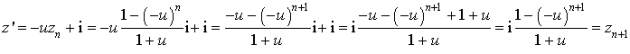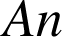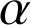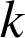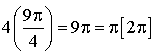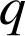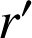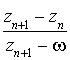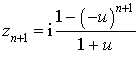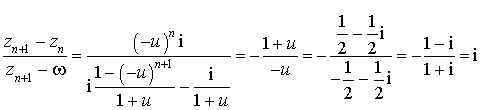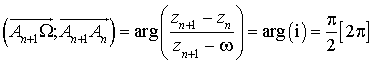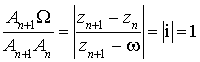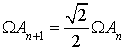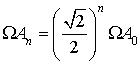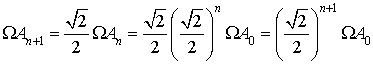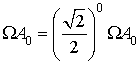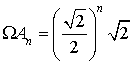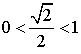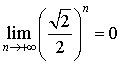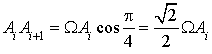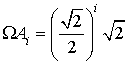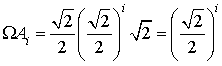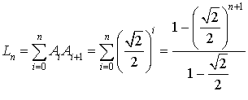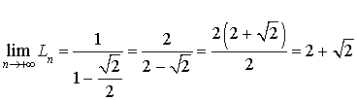Introduction
Prérequis : Cours de spécialité mathématiques sur les similitudes directes.
Durée : 120 minutes
Niveau : quelques questions difficiles
Énoncé de l'exercice
Le plan est rapporté au repère orthonormé direct 
.
Soit
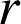un nombre réel strictement positif, 
un réel tel que 
et
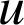le nombre complexe de module
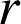dont un argument est . Pour tout entier naturel
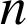, on considère les points 
définis par : 
, 
est le point d'affixe
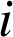et, pour 
, est l'image de 
par la similitude directe de centre 
, de rapport
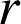et d'angle .
On note 
l'affixe de .
1)
a. Ecrire, pour tout entier , une relation entre , 
et 
.
b. Montrer par récurrence que pour tout entier 
: 
.
c. Calculer en fonction de
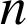et de
.
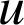2)
a. Montrer qu'il existe une unique similitude directe
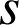telle que 
et 
, puis préciser les éléments caractéristiques de
.
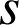b. Montrer que pour tout entier naturel
: 
.
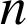c. On note 
la transformation identique du plan et, pour tout entier naturel
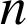, on pose : 
.
Soit
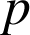un entier naturel, montrer que pour tout
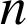de
: 
.
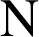3) On pose 
.
a. Montrer que 
est une homothétie.
b. En déduire que les points appartiennent à quatre droites fixes à préciser.
4) On suppose dorénavant et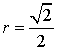 
.
a. Préciser les éléments caractéristiques de
.
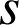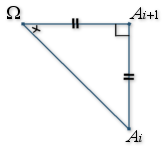
b. Montrer que, pour tout
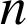de
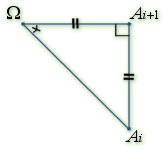
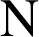, le triangle 
est rectangle isocèle direct en 
.
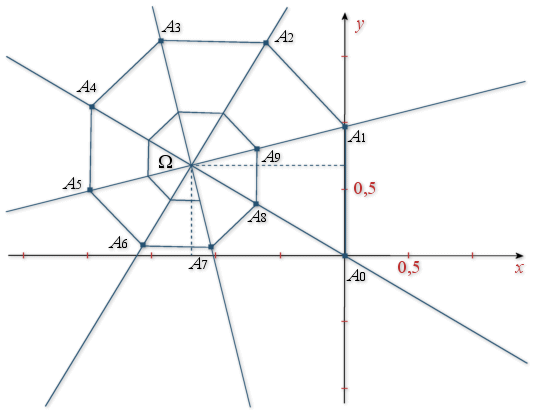
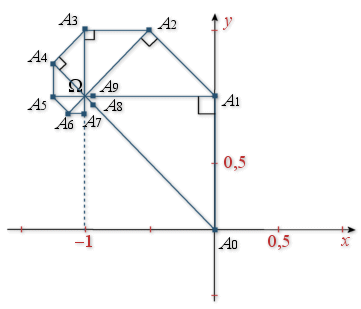
c. Représenter graphiquement les points 
puis 
en choisissant
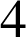cm pour unité graphique.
d. Calculer 
en fonction de
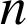. En déduire 
.
e. Soit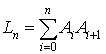 
. Calculer 
en fonction de
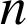puis étudier 
.
